Advertisements
Advertisements
प्रश्न
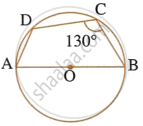
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130o. Find:
1) ∠DAB
2) ∠DBA

उत्तर
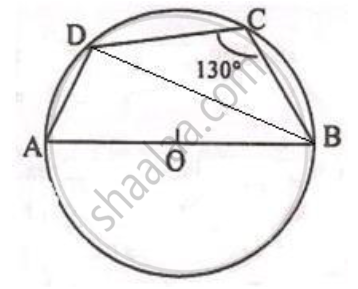
Given: AB is the diameter of the circle with centre O, ∠BCD = 130°
To find: ∠DAB, ∠DBA
1) Clearly, ABCD is a cyclic quadrilateral.
We know, the sum of a pair of opposite angles of a cyclic quadrilateral is 180°
∴ ∠DAB + ∠DCB = 180°
⇒ ∠DAB + 130° = 180°
⇒ ∠DAB = 180° - 130° = 50°
2) Consider ΔDAB,
Here, ∠ADB = 90° …..[Since angle in a semi-circle is a right angle]
So, by angle sum property of a triangle,
∠DAB + ∠DBA + ∠ADB = 180°
⇒ 50° + ∠DBA + 90° = 180°
⇒ ∠DBA = 180° - 140° = 40°
APPEARS IN
संबंधित प्रश्न
In the following figure,
- if ∠BAD = 96°, find ∠BCD and ∠BFE.
- Prove that AD is parallel to FE.

Use the given figure to find:
- ∠BAD,
- ∠DQB.
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
In the given figure, O is the centre of the circle. The tangents at B and D intersect each other at point P. If AB is parallel to CD and ∠ABC = 55°, find:
- ∠BOD
- ∠BPD
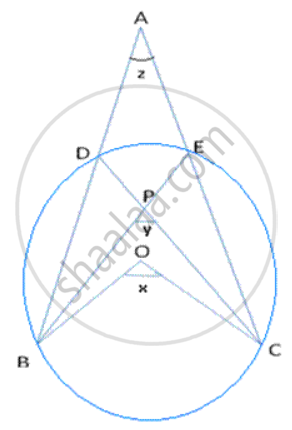
In following fig., O is the centre of the circle, prove that ∠x =∠ y + ∠ z.
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

In the figure, given below, find: ∠ADC, Show steps of your working.
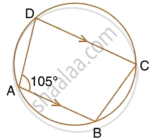
In the figure, given below, find: ∠ABC. Show steps of your working.

In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find: ∠ADB.
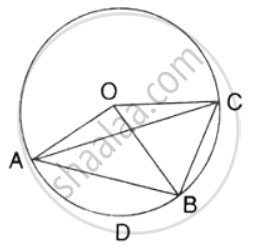
In the given figure, AB is the diameter of a circle with centre O.
∠BCD = 130°. Find:
- ∠DAB
- ∠DBA