Advertisements
Advertisements
प्रश्न
In the figure, given below, find: ∠ABC. Show steps of your working.

उत्तर
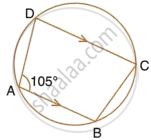
∠ADC + ∠ABC = 180°
(Sum of opposite angles of a cyclic quadrilateral is 180°)
`=>` ∠ABC = 180° – 75° = 105°
APPEARS IN
संबंधित प्रश्न
In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
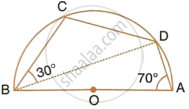
In the given figure, C and D are points on the semi-circle described on AB as diameter. Given angle BAD = 70° and angle DBC = 30°, calculate angle BDC.
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65 ° , find the remaining angles
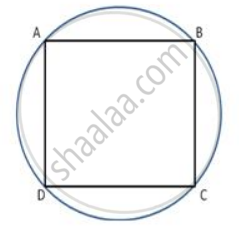
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65° , find the remaining angles.
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC
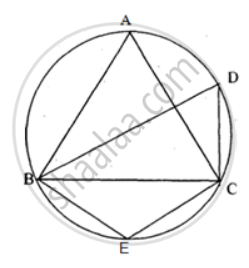
If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.
In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the value of a, b, and c.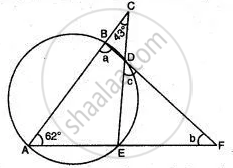
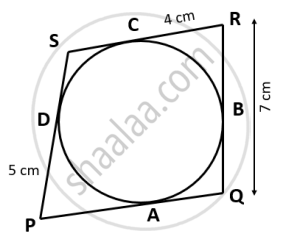
In the given figure, the sides of the quadrilateral PQRS touches the circle at A, B, C and D. If RC = 4 cm, RQ = 7 cm and PD = 5 cm. Find the length of PQ: