Advertisements
Advertisements
प्रश्न
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.
उत्तर
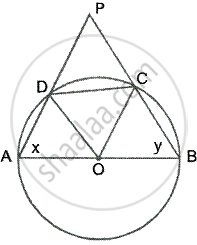
In a circle, ABCD is a cyclic quadrilateral in which AB is the diameter and chord CD is equal to the radius of the circle
To prove – ∠APB = 60°
Construction – Join OC and OD
Proof – Since chord CD = CO = DO ...[Radii of the circle]
∴ ΔDOC is an equilateral triangle
∴ ∠DOC = ∠ODC = ∠DCO = 60°
Let ∠A = x and ∠B = y
Since OA = OB = OC = OD ...[Radii of the same circle]
∴ ∠ODA = ∠OAD = x and ∠OCB = ∠OBC = y
∴ ∠AOD = 180° – 2x and ∠BOC = 180° – 2y
But AOB is a straight line
∴ ∠AOD + ∠BOC + ∠COD = 180°
`=>` 180° – 2x + 180° – 2y + 60° = 180°
`=>` 2x + 2y = 240°
`=>` x + y = 120°
But ∠A + ∠B + ∠P = 180° ...[Angles of a triangle]
`=>` 120° + ∠P = 180°
`=>` ∠P = 180° – 120°
`=>` ∠P = 60°
Hence ∠APB = 60°
APPEARS IN
संबंधित प्रश्न
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of:
- ∠BCD
- ∠BOD
- ∠OBD

PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
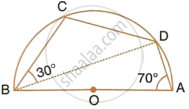
In the given figure, C and D are points on the semi-circle described on AB as diameter. Given angle BAD = 70° and angle DBC = 30°, calculate angle BDC.
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
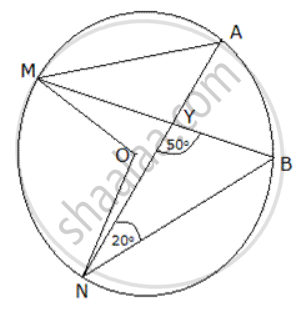
MABN are points on a drde having centre O. AN and MB cut at Y. If ∠ NYB = 50" and ∠ YNB = 200, find ∠ MAN and reflex angle MON.
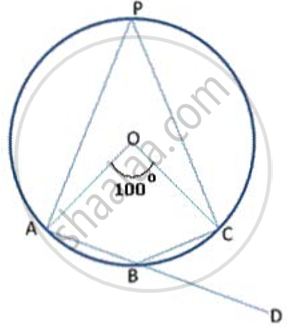
In following fig., O is the centre of the circle. Find ∠ CBD.
In the figure, given below, find: ∠ABC. Show steps of your working.

