Advertisements
Advertisements
प्रश्न
ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
उत्तर
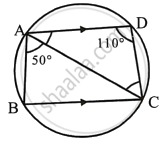
ABCD is a cyclic quadrilateral in which AD || BC
∠ADC = 110°, ∠BAC = 50°
∠B + ∠D = 180°
(Sum of opposite angles of a quadrilateral)
`=>` ∠B + 110° = 180°
`=>` ∠B = 70°
Now in ΔABC,
∠BAC + ∠ABC + ∠ACB = 180°
`=>` 50° + 70° + ∠ACB = 180°
`=>` ∠ACB = 180° – 120° = 60°
∵ AD || BC
∴ ∠DAC = ∠ACB = 60° ...(Alternate angles)
Now in ΔADC,
∠DAC + ∠ADC + ∠DCA = 180°
`=>` 60° + 110° + ∠DCA = 180°
`=>` ∠DCA = 180° – 170° = 10°
APPEARS IN
संबंधित प्रश्न
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130o. Find:
1) ∠DAB
2) ∠DBA

ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate:
- ∠BEC
- ∠BED
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B. If ∠A : ∠B = 2 : 1; find angles A and B.
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.
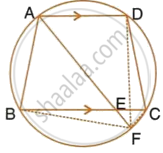
If the bisector of angle A meets BC at point E and the given circle at point F, prove that:
- EF = FC
- BF = DF
ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC=120°.
Calculate: ∠ BED.
In the following figure, Prove that AD is parallel to FE.

ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q. Show that quadrilateral PCDQ is cyclic.
The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backward bisects the opposite side.
