Advertisements
Advertisements
प्रश्न
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.
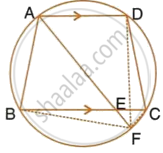
If the bisector of angle A meets BC at point E and the given circle at point F, prove that:
- EF = FC
- BF = DF
उत्तर
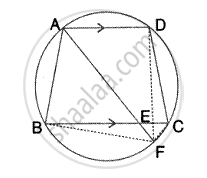
Given – ABCD is a cyclic quadrilateral in which AD || BC.
Bisector of ∠A meets BC at E and the given circle at F.
DF and BF are joined.
To prove –
- EF = FC
- BF = DF
Proof – ABCD is a cyclic quadrilateral and AD || BC
∵ AF is the bisector of ∠A, ∠BAF = ∠DAF
Also, ∠DAE = ∠BAE
∠DAE = ∠AEB ...[Alternate angles]
i. In ΔABE, ∠ABE = 180° – 2∠AEB
∠CEF = ∠AEB ...[Vertically opposite angles]
∠ADC = 180° – ∠ABC
= 180° – (180° – 2∠AEB)
∠ADC = 2∠AEB
∠AFC = 180° – ∠ADC
= 180° – 2∠AEB ...[Since ADFC is a cyclic quadrilateral]
∠ECF = 180° – (∠AFC + ∠CEF)
= 180° – (180° – 2∠AEB + ∠AEB)
= ∠AEB
∴ EF = FC
ii. ∴ Arc BF = Arc DF ...[Equal arcs subtends equal angles]
`=>` BF = DF ...[Equal arcs have equal chords]
Hence proved.
APPEARS IN
संबंधित प्रश्न
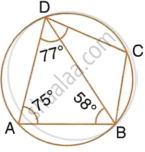
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
- ∠BDC,
- ∠BCD,
- ∠BCA.
Use the given figure to find:
- ∠BAD,
- ∠DQB.
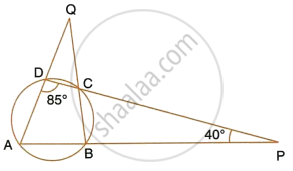
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
If two non-parallel sides of a trapezium are equal, it is cyclic. Prove it. Or An isosceles trapezium is always cyclic. Prove it.
The bisectors of the opposite angles A and C of a cydic quadrilateral ABCD intersect the cirde at the points E and F, respectively. Prove that EF is a diameter of the circle.
In following fig., O is the centre of the circle. Find ∠ CBD.
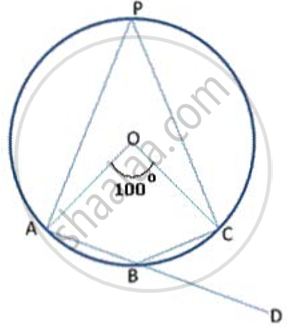
In the following figure, O is the centre of the circle. Find the values of a, b and c.
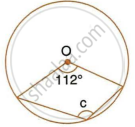
In the figure, given below, find: ∠ABC. Show steps of your working.

Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
If O is the centre of the circle, find the value of x in each of the following figures