Advertisements
Advertisements
प्रश्न
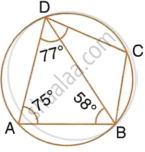
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
- ∠BDC,
- ∠BCD,
- ∠BCA.
उत्तर
i. By angle – sum property of triangle ABD,
∠BAD + ∠ABD + ∠ADB = 180°
133° + ∠ADB = 180°
∠ADB = 180° – 133°
∠ADB = 47°
∴ ∠ADC = ∠ADB + ∠BDC
∴ 77° = 47° + ∠BDC
∴ 77° – 47° = ∠BDC
∴ ∠BDC = 30°
ii. ∠BAD + ∠BCD = 180° ...(Sum of opposite angles of a cyclic quadrilateral is 180°)
`=>` ∠BCD = 180° – 75° = 105°
∴ ∠BCD = 105°
iii. ∠BCA = ∠BDA = 47° ...(Angle subtended by the same chord on the circle are equal)
APPEARS IN
संबंधित प्रश्न
In the figure, given below, find:
- ∠BCD,
- ∠ADC,
- ∠ABC.
Show steps of your working.

ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°; find ∠BAC.

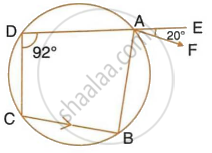
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Give reason in support of your answer.
Prove that any four vertices of a regular pentagon are concylic (lie on the same circle).
In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
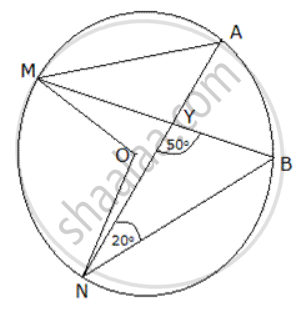
MABN are points on a drde having centre O. AN and MB cut at Y. If ∠ NYB = 50" and ∠ YNB = 200, find ∠ MAN and reflex angle MON.
Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC=120°.
Calculate: ∠ BED.
In the figure, given below, find: ∠ADC, Show steps of your working.
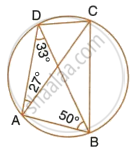
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠CAB.