Advertisements
Advertisements
प्रश्न
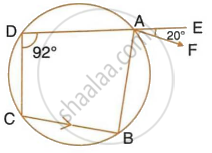
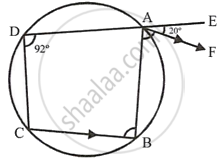
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Give reason in support of your answer.
उत्तर
In cyclic quad. ABCD,
AF || CB and DA is produced to E such that ∠ADC = 92° and ∠FAE = 20°
Now, we need to find the measure of ∠BCD
In cyclic quad. ABCD,
`=>` ∠B + ∠D = 180°
`=>` ∠B + 92° = 180°
`=>` ∠B = 180° – 92°
`=>` ∠B = 88°
Since AF || CB, ∠FAB = ∠B = 88°
But, ∠FAE = 20° ...[Given]
Ext. ∠BAE = ∠BAF + ∠FAE
= 88° + 20°
= 108°
But, Ext. ∠BAE = ∠BCD
∴ ∠BCD = 108°
APPEARS IN
संबंधित प्रश्न
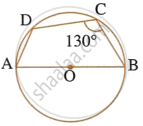
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130o. Find:
1) ∠DAB
2) ∠DBA

In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°.
Calculate:
- ∠DBC,
- ∠DCB,
- ∠CAB.

ABCD is a quadrilateral inscribed in a circle, having ∠ = 60°; O is the center of the circle.
Show that: ∠OBD + ∠ODB =∠CBD +∠CDB.
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

In a square ABCD, its diagonals AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and the bisector of angle ABD meets AC at N and AM at L. Show that:
- ∠ONL + ∠OML = 180°
- ∠BAM + ∠BMA
- ALOB is a cyclic quadrilateral.
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

In the following figure, Prove that AD is parallel to FE.

Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
In the given figure, AB is the diameter of a circle with centre O.
∠BCD = 130°. Find:
- ∠DAB
- ∠DBA
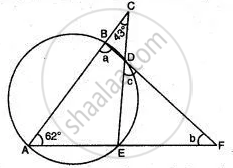
In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the value of a, b, and c.