Advertisements
Advertisements
प्रश्न
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
उत्तर
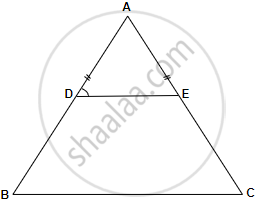
Given – In ∆ABC, AB = AC and D and E are points on AB and AC such that AD = AE. DE is joined.
To prove – B, C, E, D are concyclic.
Proof – In ∆ABC, AB = AC
∴ ∠B = ∠C ...[Angles opposite to equal sides]
Similarly, In ∆ADE, AD = AE ...[Given]
∴ ∠ADE = ∠AED ...[Angles opposite to equal sides]
In ∆ABC,
∴ `(AD)/(AB) = (AE )/(AC)`
∴ DE || BC
∴ ∠ADE = ∠B ...[Corresponding angles]
But ∠B = ∠C ...[Proved]
∴ Ext ∠ADE = Its interior opposite ∠C
∴ BCED is a cyclic quadrilateral
Hence B, C, E and D are concyclic.
APPEARS IN
संबंधित प्रश्न
In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find;
- ∠DBC
- ∠BCP
- ∠ADB
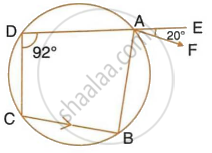
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Give reason in support of your answer.
In triangle ABC, AB = AC. A circle passing through B and c intersects the sides AB and AC at D and E respectively. Prove that DE || BC.
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

In following fig., O is the centre of the circle. Find ∠ CBD.
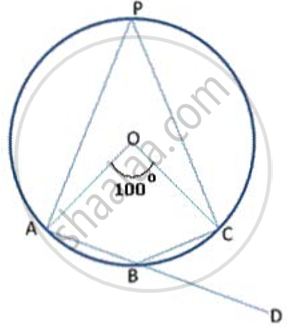
In the following figure, Prove that AD is parallel to FE.

In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC
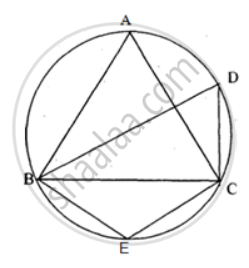
Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
In the given figure O is the center of the circle, ∠ BAD = 75° and chord BC = chord CD. Find:
(i) ∠BOC (ii) ∠OBD (iii) ∠BCD.