Advertisements
Advertisements
प्रश्न
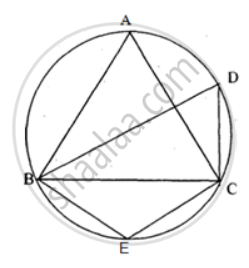
In triangle ABC, AB = AC. A circle passing through B and c intersects the sides AB and AC at D and E respectively. Prove that DE || BC.
उत्तर १

To prove = DE II BC
Proof: In cydic quadrilateral DECB
∠ DEC + ∠ DBC = 80° - ( 1) (Opposite angles of cyclic quadrilateral)
Also, ∠ AED + ∠ DEC = 80° - (2) (Linear pair)
From (1) and (2), we get,
∠ DBC = ∠ AED - (3)
AB= AC (given)
∴ ∠ABC = ∠ ACB - (4) (angles opposite to equal sides of triangle)
From (3) and ( 4) ⇒ ∠ AED = ∠ ACB
But, these are corresponding angles
∴ DE II BC
उत्तर २
In order to prove that DE || BC, it is sufficient to show that ∠B = ∠ADE.
In Δ ABC, we have
AB = AC ⇒ ∠B = ∠C ...(i)
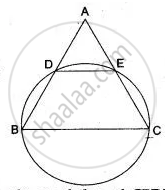
In the cyclic quadrilateral CBDE, side BD is produced to A.
∴ ∠ADE = ∠C ...(ii)( ∵ Exterior angle = Opposite interior angle )
From (i) and (ii), we get
∠B = ∠ADE.
Hence, DE || BC. ...Hence proved.
APPEARS IN
संबंधित प्रश्न
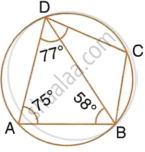
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
- ∠BDC,
- ∠BCD,
- ∠BCA.
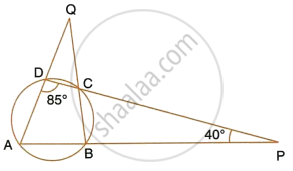
Use the given figure to find:
- ∠BAD,
- ∠DQB.
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
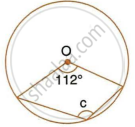
In the following figure, O is the centre of the circle. Find the values of a, b and c.
In the following figure, Prove that AD is parallel to FE.

In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

ABCD is a cyclic quadrilateral AB and DC are produced to meet in E. Prove that Δ EBC ∼ Δ EDA.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

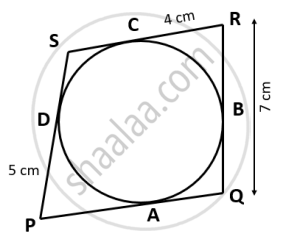
In the given figure, the sides of the quadrilateral PQRS touches the circle at A, B, C and D. If RC = 4 cm, RQ = 7 cm and PD = 5 cm. Find the length of PQ: