Advertisements
Advertisements
प्रश्न
In the following figure, Prove that AD is parallel to FE.

उत्तर

Now, ∠BAD + ∠BFE
= 96 °+ 84°
= 180°
But these two are interior angles on the same side of a pair of lines AD and FE
∴ AD || FE
APPEARS IN
संबंधित प्रश्न
In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC=120°.
Calculate: ∠ BED.
In the given below figure,
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
Find: (i) ∠ BCD, (ii) ∠ ADB.
Hence show that AC is a diameter.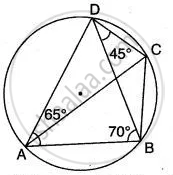
In the figure , Δ PQR is an isosceles triangle with PQ = PR, and m ∠ PQR = 35°. Find m ∠ QSR and ∠ QTR.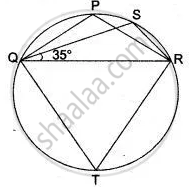
An exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle, to prove the theorem complete the activity.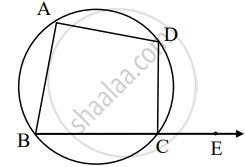
Given: ABCD is cyclic,
`square` is the exterior angle of ABCD
To prove: ∠DCE ≅ ∠BAD
Proof: `square` + ∠BCD = `square` .....[Angles in linear pair] (I)
ABCD is a cyclic.
`square` + ∠BAD = `square` ......[Theorem of cyclic quadrilateral] (II)
By (I) and (II)
∠DCE + ∠BCD = `square` + ∠BAD
∠DCE ≅ ∠BAD
