Advertisements
Advertisements
प्रश्न
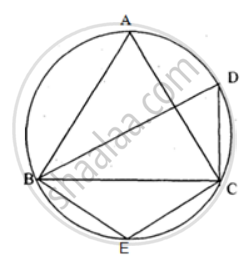
In the figure , Δ PQR is an isosceles triangle with PQ = PR, and m ∠ PQR = 35°. Find m ∠ QSR and ∠ QTR.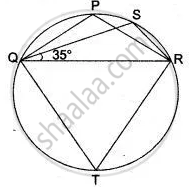
उत्तर
In ΔPQR, We have
PQ = PR
⇒ ∠ PQR = ∠ PRQ
⇒ ∠ PRQ = 35°
∴ ∠ QPR = 180° - ( ∠ PQR + ∠ PRQ)
∴ ∠ QPR = 180° - ( 35° + 35°) = 110°
Since PQTR is a cyclic quadrilateral.
∴ ∠ P + ∠ T = 180°
∴ ∠ T = 180° - 110° = 70°.
In cyclic quadrilateral QSRT, we have
∴ ∠ S + ∠ T = 180°
⇒ ∠ S = 180° - 70° = 110°.
APPEARS IN
संबंधित प्रश्न
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of:
- ∠BCD
- ∠BOD
- ∠OBD

PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

In the given figure, AB = AC. Prove that DECB is an isosceles trapezium.
In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find;
- ∠DBC
- ∠BCP
- ∠ADB
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.
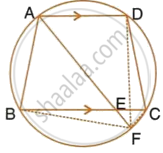
If the bisector of angle A meets BC at point E and the given circle at point F, prove that:
- EF = FC
- BF = DF
In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BEC
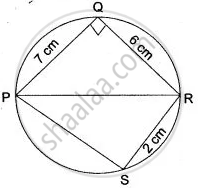
In the figure alongside PR is a diameter of the circle, PQ = 7 cm; QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.