Advertisements
Advertisements
प्रश्न
In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
उत्तर
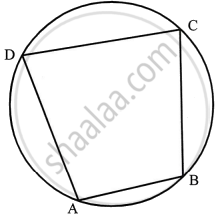
ABCD is a cyclic quadrilateral.
∴ ∠A + ∠C = 180°
`=>` 3∠C + ∠C = 180°
`=>` 4∠C = 180°
`=>` ∠C = 45°
∵ ∠A = 3∠C
`=>` ∠A = 3 × 45°
`=>` ∠A = 135°
Similarly,
∴ ∠B + ∠D = 180°
`=>` ∠B + 5∠B = 180°
`=>` 6∠B = 180°
`=>` ∠B = 30°
∵ ∠D = 5∠B
`=>` ∠D = 5 × 30°
`=>` ∠D = 150°
Hence, ∠A = 135°, ∠B = 30°, ∠C = 45°, ∠D = 150°
APPEARS IN
संबंधित प्रश्न
In the figure, given below, find:
- ∠BCD,
- ∠ADC,
- ∠ABC.
Show steps of your working.

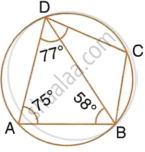
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
- ∠BDC,
- ∠BCD,
- ∠BCA.
In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find;
- ∠DBC
- ∠BCP
- ∠ADB
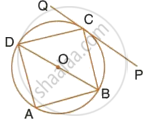
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.
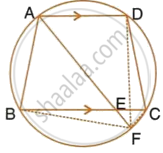
If the bisector of angle A meets BC at point E and the given circle at point F, prove that:
- EF = FC
- BF = DF
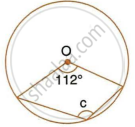
In the following figure, O is the centre of the circle. Find the values of a, b and c.
In the following figure, Prove that AD is parallel to FE.

In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.