Advertisements
Advertisements
प्रश्न
Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
उत्तर
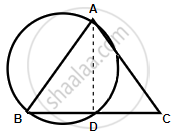
Join AD.
AB is the diameter.
∴ ∠ADB = 90° ...(Angle in a semi-circle)
But, ∠ADB + ∠ADC = 180° ...(Linear pair)
`=>` ∠ADC = 90°
In ΔABD and ΔACD,
∠ADB = ∠ADC ...(Each 90°)
AB = AC ...(Given)
AD = AD ...(Common)
ΔABD ≅ ΔACD ...(RHS congruence criterion)
`=>` BD = DC ...(C.P.C.T)
Hence, the circle bisects base BC at D.
APPEARS IN
संबंधित प्रश्न
The common point of a tangent to a circle and the circle is called ______.
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
The length of the direct common tangent to two circles of radii 12cm and 4cm is 15cm. calculate the distance between their centres.
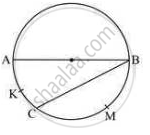
In the following figure, seg AB is a diameter of the circle, m (arc AKC) = 40°. Find the value of m (arc BMC).
Find the area of sector whose central angle and radius are 60o and 21 cm respectively.
`(pi = 22/7)`
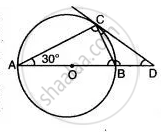
In Figure, AB is diameter and AC is a chord of a circle such that ∠BAC = 30°. The tangent at C intersects AB produced at D. Prove that BC = BD.
Two parallel lines touch the circle at
points A and B respectively. If the area of the circle is 25 n cm2, then AB is equal to ______
A: What is a line called, if it meets the circle at only one point?
B: Collection of all points equidistant from a fixed point is ______.
- Chord
- Tangent
- Circle
- Curve
- Secant
Which is correct matching?
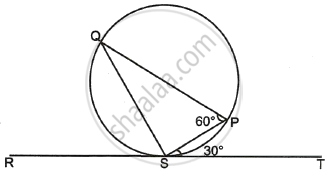
In the given diagram RT is a tangent touching the circle at S. If ∠PST = 30° and ∠SPQ = 60°, then ∠PSQ is equal to ______.
In the given figure O, is the centre of the circle. CE is a tangent to the circle at A. If ∠ABD = 26° find:
- ∠BDA
- ∠BAD
- ∠CAD
- ∠ODB

