Advertisements
Advertisements
प्रश्न
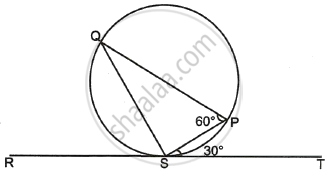
In the given diagram RT is a tangent touching the circle at S. If ∠PST = 30° and ∠SPQ = 60°, then ∠PSQ is equal to ______.
पर्याय
40°
30°
60°
90°
उत्तर
In the given diagram RT is a tangent touching the circle at S. If ∠PST = 30° and ∠SPQ = 60°, then ∠PSQ is equal to 90°.
Explanation:

∠PQS = ∠PST ...(∠S in alternate segment)
= 30°
In ΔPQS,
∠PQS + ∠PSQ + ∠SPQ = 180°
30° + ∠PSQ + 60° = 180°
∠PSQ = 180° – 90°
= 90°
APPEARS IN
संबंधित प्रश्न
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
If the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is 60°, then find the length of OP
In the given figure O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of a circle.

In the given figure O is the centre of the circle. Tangents A and B meet at C. If ∠ACO = 30°, find
1) ∠BCO
2) ∠AOB
3) ∠APB
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
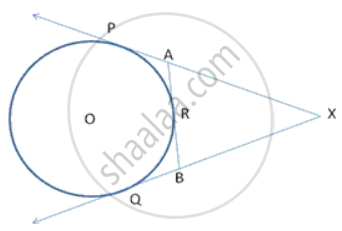
In the figure, XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that XA + AR = XB + BR.
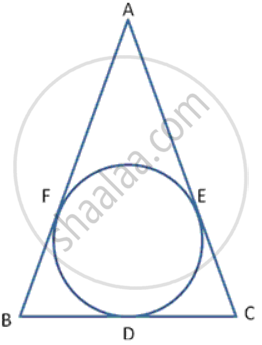
In following figure , the incircle of Δ ABC , touches the sides BC , CA and AB at D , E and F respectively. Show AF + BD + CE = AE + BF + CD
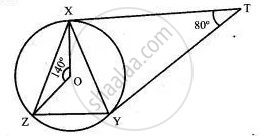
In the alongside, figure, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°. Calculate the value of ∠ZXY.
A circle of radius 5.2 cm has two tangents AB and CD parallel to each other. What is the distance between the two tangents?
If O is centre of a circle and Chord PQ makes an angle 50° with the tangent PR at the point of contact P, then the angle subtended by the chord at the centre is ______.