Advertisements
Advertisements
प्रश्न
In the given figure O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of a circle.

उत्तर
Let OD = OC = x cm (radius of same circle)
Since ACD is a secant and AB is a tangent to the given circle, we have,
AC . AD = AB2
(7.5)(7.5 + 2x) = 152
⇒ 56.25 + 15x = 225
⇒ 15x = 168.75 ⇒ x = 11.25
Thus, the radius of the circle is 11.25 cm.
APPEARS IN
संबंधित प्रश्न
In Fig. 1, PQ is a tangent at a point C to a circle with centre O. if AB is a diameter and ∠CAB = 30°, find ∠PCA.

The common point of a tangent to a circle and the circle is called ______.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

The given figure shows a circle with centre O and BCD is tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.

In the given figure, find TP if AT = 16 cm and AB = 12 cm.

In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find AB.

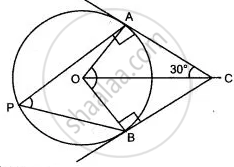
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°,
find: (i) ∠ BCO (ii) ∠ AOB (iii) ∠ APB
In Question 5 above, if radii of the two circles are equal, prove that AB = CD.
Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
A tangent JK is drawn to a circle with centre C such that CK = 6 cm and ∠CKJ = 60°. Find the length of the tangent JK.

