Advertisements
Advertisements
प्रश्न
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°,
find: (i) ∠ BCO (ii) ∠ AOB (iii) ∠ APB
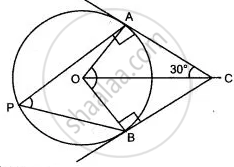
उत्तर
(i) ∠ BCO = ∠ ACO = 30° .....( ∴ C is the intersecting point of tangents AC and BC)
(ii) ∠ OAC = ∠ OBC = 90°
∠ ACO = 30° .....(Given)
∠ AOC = ∠ BOC = 180° - (90° + 30°) ....(Sum of the angles of a Δ is 180°)
∠ AOC = 180° - 120°
∠ AOC = 60°
∠ AOB = ∠ AOC + ∠ BOC
∠ AOB = 60° + 60° = 120°
(iii) ∠ APB = `1/2"∠ AOB" = (120°)/2 = 60°` .....( ∴ Angle substended at the remaining part of the circle is half the ∠ substended at the centre)
APPEARS IN
संबंधित प्रश्न
A line intersecting a circle in two points is called a ______.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is ______.
Draw a circle of radius 3.5 cm. Marks a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
The given figure shows a circle with centre O and BCD is tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.

In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find the length of tangent PT.

Construct a tangent to a circle with centre O and radius 3.5 cm at a point P on it.
If PA and PB are two tangents drawn from a point P to a circle with center C touching it A and B, prove that CP is the perpendicular bisector of AB.
Two circle with radii r1 and r2 touch each other externally. Let r be the radius of a circle which touches these two circle as well as a common tangent to the two circles, Prove that: `1/sqrtr + 1/sqrtr_1 + 1/sqrtr_2`.
Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
In the given figure O, is the centre of the circle. CE is a tangent to the circle at A. If ∠ABD = 26° find:
- ∠BDA
- ∠BAD
- ∠CAD
- ∠ODB

