Advertisements
Advertisements
प्रश्न
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is ______.
पर्याय
12 cm
13 cm
8.5 cm
`sqrt119` cm
उत्तर
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is `bbunderline(sqrt119 cm)`.
Explanation:
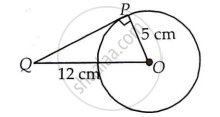
Suppose there is a circle whose center is O.
In right ΔQPO,
According to Pythagoras theorem,
OQ2 = OP2 + PQ2
= PQ = `sqrt(OQ^2 - OP^2)`
= PQ = `sqrt(12^2 - 5^2)`
= PQ = `sqrt(144 - 25`
= PQ = `sqrt119` cm.
APPEARS IN
संबंधित प्रश्न
How many tangents can a circle have?
In the following figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
In fig. 5 is a chord AB of a circle, with centre O and radius 10 cm, that subtends a right angle at the centre of the circle. Find the area of the minor segment AQBP. Hence find the area of major segment ALBQA. (use π = 3.14)

Draw Δ ABC such that, AB = 8 cm, BC = 6 cm and ∠ B = 90°. Draw seg BD
perpendicular to hypotenuse AC. Draw a circle passing through points
B, D, A. Show that line CB is a tangent of the circle.
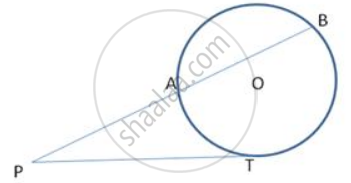
In fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = 5 cm, find PT.
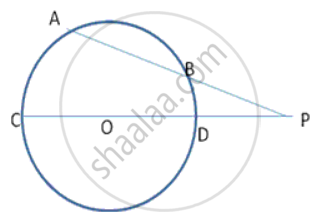
In fig., AB and DC are two chords of a circle with centre O. these chords when produced meet at P. if PB = Bern, BA = 7cm and PO = 14.5cm, find the radius of the circle.
In the following figure, seg AB is a diameter of the circle, m (arc AKC) = 40°. Find the value of m (arc BMC).
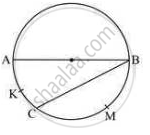
In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)

At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is ______
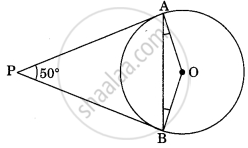
In the figure, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to ______.
Tangents from an external point to a circle are ______
In the following figure, PA and PB are tangents from a point P to a circle with centre O. Then the quadrilateral OAPB must be a ______

In the given figure, PT is a tangent to the circle at T, chord BA is produced to meet the tangent at P. Perpendicular BC bisects the chord TA at C. If PA = 9 cm and TB = 7 cm, find the lengths of:
- AB
- PT
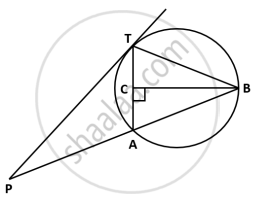
ΔABC circumscribes a circle of radius r such that ∠B = 90°. If AB = 3 cm and BC = 4 cm, then find the value of r.
In the given figure, PA is a tangent to the circle drawn from the external point P and PBC is the secant to the circle with BC as diameter. If ∠AOC = 130°, then find the measure of ∠APB, where O is the centre of the circle.

In the given figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 25°, then x is equal to ______.

How many tangents can be drawn to a circle from a point on it?
A circle of radius 5.2 cm has two tangents AB and CD parallel to each other. What is the distance between the two tangents?
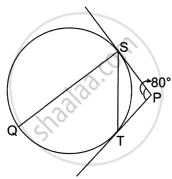
In the given diagram, PS and PT are the tangents to the circle. SQ || PT and ∠SPT = 80°. The value of ∠QST is ______.