Advertisements
Advertisements
प्रश्न
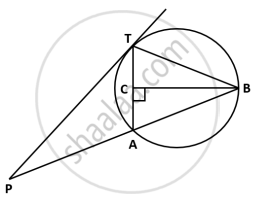
In the given figure, PT is a tangent to the circle at T, chord BA is produced to meet the tangent at P. Perpendicular BC bisects the chord TA at C. If PA = 9 cm and TB = 7 cm, find the lengths of:
- AB
- PT
उत्तर
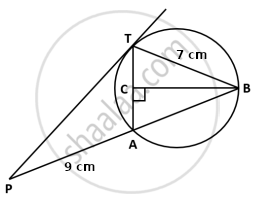
Given: In diagram PT is tangent BC bisects TA at right angles.
BT = 7 cm, PA = 9 cm
(a) Line segment BC is a common side of both the ΔACB and ΔTCB.
ΔACB is 90° then ΔTCB also is 90°.
Hence the length of BT and the length of AB will be the same.
∴ Length of BT is 7 cm then length of AB is also 7 cm.
(b) PT2 = PA × PB
PT2 = 9 × (9 + 7)
PT2 = 9 × 16
PT = `sqrt(9 xx 16)`
PT = 3 × 4
PT = 4 cm
APPEARS IN
संबंधित प्रश्न
Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
In fig. 5 is a chord AB of a circle, with centre O and radius 10 cm, that subtends a right angle at the centre of the circle. Find the area of the minor segment AQBP. Hence find the area of major segment ALBQA. (use π = 3.14)

In Figure 5, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR = 189 cm2, then find the lengths of sides PQ and PR.
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (ii) radius of the circle.

In following fig., a circle is touching the side BC of Δ ABC at P and AB and AC produced at Q and R respectively. Prove that AQ is half the perimeter of Δ ABC.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate : ∠CDB

Two circle with radii r1 and r2 touch each other externally. Let r be the radius of a circle which touches these two circle as well as a common tangent to the two circles, Prove that: `1/sqrtr + 1/sqrtr_1 + 1/sqrtr_2`.
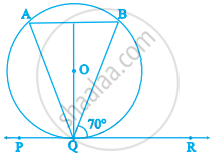
In figure, if PQR is the tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to ______.
In the following figure, PA and PB are tangents from a point P to a circle with centre O. Then the quadrilateral OAPB must be a ______

The distance between two tangents parallel to each other of a circle is 13 cm. Find the radius of the circle.
