Advertisements
Advertisements
प्रश्न
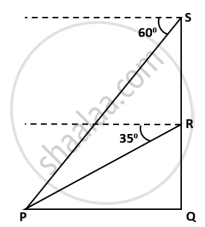
A drone camera is used to shoot an object P from two different positions R and S along the same vertical line QRS. The angle of depression of the object P from these two positions is 35° and 60° respectively as shown in the diagram. If the distance of the object P from point Q is 50 metres, then find the distance between R and S correct to the nearest meter.
उत्तर
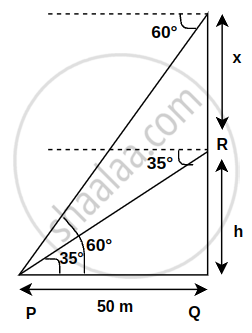
In ΔPQR,
tan 35° = `"QR"/"PQ" = "QR"/50`
∴ QR = 50 × tan 35°
= 50 × 0.7002
= 5 × 7.002
= 35.010 m
In ΔSQP,
tan 60° = `"SQ"/"PQ" = "SQ"/50`
∴ SQ = tan 60° × 50
= `50 sqrt3`
= 50 × 1.732
= 5 × 17.32
= 86.60
SR = SQ - QR
SR = 86.60 - 35.01
SR = 51.59 m
SR = 52 m
The distance between R and S is correct to the nearest 52 meters.
APPEARS IN
संबंधित प्रश्न
An aeroplane at an altitude of 1500 metres, finds that two ships are sailing towards it in the same direction. The angles of depression as observed from the aeroplane are 45° and 30° respectively. Find the distance between the two ships
The angle of elevation of the top of a tower, from a point on the ground and at a distance of 160 m from its foot, is found to be 60°. Find the height of the tower.
A kite is attached to a string. Find the length of the string, when the height of the kite is 60 m and the string makes an angle 30° with the ground.
The upper part of a tree, broken over by the wind, makes an angle of 45° with the ground and the distance from the root to the point where the top of the tree touches the ground is 15 m. What was the height of the tree before it was broken?
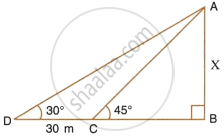
In the figure, given below, it is given that AB is perpandiculer to BD and is of length X metres. DC = 30 m, ∠ADB = 30° and ∠ACB = 45°. Without using tables, find X.
The radius of a circle is given as 15 cm and chord AB subtends an angle of 131° at the centre C of the circle. Using trigonometry, calculate:
- the length of AB;
- the distance of AB from the centre C.
As observed from the top of a 80 m tall lighthouse, the angles of depression of two ships, on the same side of a light house in a horizontal line with its base, are 30° and 40° respectively. Find the distance between the two ships. Give your answer corrected to the nearest metre.
A kite tied to a string makes an angle of 60° with the ground. Find the perpendicular height of the kite if the length of its string is 250 m.
A boy is 1.54 m tall. Standing at a distance of 3m in front of a 4.54 m high wall he can just manage to see the sun. Find the angle of elevation of the sun.
A man in a boat rowing away from a lighthouse 180 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° and 30°. Find the speed of the boat.
