Advertisements
Advertisements
प्रश्न
A kite tied to a string makes an angle of 60° with the ground. Find the perpendicular height of the kite if the length of its string is 250 m.
उत्तर

Let K be the kite and the string is tied to point P on ground.
In ΔKLP
`"KL"/"KP"` = `sin60^circ`
`h/250 = sqrt(3)/2`
`h = (250sqrt(3))/2 = 125sqrt(3)`
Thus , the perpendicular height of the kite is `125sqrt(3)` m .
APPEARS IN
संबंधित प्रश्न
An aeroplane at an altitude of 1500 metres, finds that two ships are sailing towards it in the same direction. The angles of depression as observed from the aeroplane are 45° and 30° respectively. Find the distance between the two ships
The angle of elevation from a point P of the top of a tower QR, 50 m high is 60o and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre

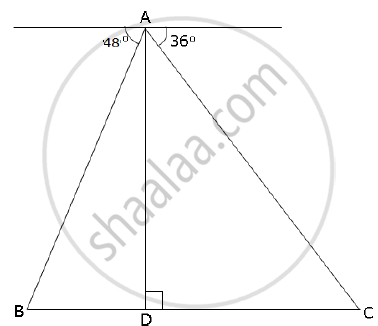
From the top of a lighthouse, 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.
The height of a tree is `sqrt(3)` times the length of its shadow. Find the angle of elevation of the sun.
The horizontal distance between two towers is 75 m and the angular depression of the top of the first tower as seen from the top of the second, which is 160 m high, is 45°. Find the height of the first tower.
The length of the shadow of a tower standing on level plane is found to be 2y metres longer when the sun’s altitude is 30° than when it was 45°. Prove that the height of the tower is `y(sqrt(3) + 1)` metres.
A vertical tower is 20 m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower?
The height of an observation tower is 180m above sea level. A ship coming towards the tower is observed at an angle of depression of 30°. Calculate the distance of the boat from the foot of the observation tower.
A flagstaff stands on a vertical pole. The angles of elevation of the top and the bottom of the flagstaff from a point on the ground are found to be 60° and 30° respectively. If the height of the pole is 2.5m. Find the height of the flagstaff.
A vertical tower standing on a horizontal plane is surmounted by a vertical flagstaff. At a point 100 m away from the foot of the tower, the angle of elevation of the top and bottom of the flagstaff are 54° and 42° respectively. Find the height of the flagstaff. Give your answer correct to nearest metre.

