Advertisements
Advertisements
प्रश्न
A kite tied to a string makes an angle of 60° with the ground. Find the perpendicular height of the kite if the length of its string is 250 m.
उत्तर

Let K be the kite and the string is tied to point P on ground.
In ΔKLP
`"KL"/"KP"` = `sin60^circ`
`h/250 = sqrt(3)/2`
`h = (250sqrt(3))/2 = 125sqrt(3)`
Thus , the perpendicular height of the kite is `125sqrt(3)` m .
APPEARS IN
संबंधित प्रश्न
An aeroplane at an altitude of 1500 metres, finds that two ships are sailing towards it in the same direction. The angles of depression as observed from the aeroplane are 45° and 30° respectively. Find the distance between the two ships
The height of a tree is `sqrt(3)` times the length of its shadow. Find the angle of elevation of the sun.
In the following diagram, AB is a floor-board; PQRS is a cubical box with each edge = 1 m and ∠B = 60°. Calculate the length of the board AB.
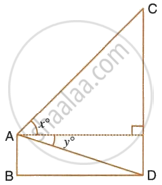
From a window A, 10 m above the ground the angle of elevation of the top C of a tower is x°, where tan `x^circ = 5/2` and the angle of depression of the foot D of the tower is y°, where tan `y^circ = 1/4`. Calculate the height CD of the tower in metres.
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second is 30° and 24° respectively. Find the height of the two towers. Give your answers correct to 3 significant figures.

The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
From the top of a 60m high building the angles of depression of the top and bottom of a lamp post are 30° and 60° respectively. Find the distance on the ground between the building and the lamp post and the difference in their heights.
The angle of elevation of a tower from a point in line with its base is `45^circ` . On moving 20m towards the tower , the angle of elevation changes to `60^circ` . Find the height of the tower.
The angle of elevation of a cloud from a point 60m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
Two men on either side of a temple 75 m high observed the angle of elevation of the top of the temple to be 30° and 60° respectively. Find the distance between the two men.
