Advertisements
Advertisements
प्रश्न
The angle of elevation of a cloud from a point 60m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
उत्तर
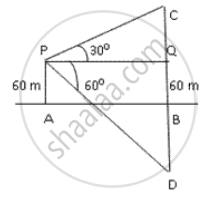
Let C be the cloud and D be its reflection . Let the height of the cloud is h metres .
BC = BD = h
BQ = AP = 60m
∴ CQ = h - 60 and DQ = h + 60
In ΔCQP,
`"PQ"/"CQ" = cot30^circ`
⇒ `"PQ"/("h" - 60) = sqrt(3)`
⇒ `"PQ" = sqrt(3)("h" - 60)"` ....(i)
In ΔDQP,
`"PQ"/"DQ" = cot60^circ`
⇒ `"PQ"/("h" + 60) = 1/sqrt(3)`
⇒ `"PQ" = 1/sqrt(3)("h" + 60)` ..(ii)
From (i) and (ii),
⇒ `sqrt(3)("h" - 60) = 1/sqrt(3)("h" + 60)`
⇒ 3h - 180 = h + 60
⇒ 2h = 240
⇒ h = 120
Thus , the height of the cloud is 120 m.
APPEARS IN
संबंधित प्रश्न
A bus covers a distance of 240 km at a uniform speed. Due to heavy rain, its speed gets reduced by 10 km/h and as such it takes two hrs longer to cover the total distance. Assuming the uniform speed to be ‘x’ km/h, form an equation and solve it to evaluate ‘x’.
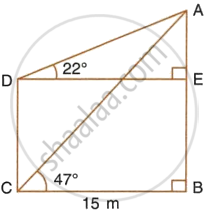
From the figure, given below, calculate the length of CD.
From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and the angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second is 30° and 24° respectively. Find the height of the two towers. Give your answers correct to 3 significant figures.

A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60° and the angle of depression of the bottom of the tower is 30°. Find:
- the height of the tower, if the height of the pole is 20 m;
- the height of the pole, if the height of the tower is 75 m.
A 1.4m tall boy stands at a point 50m away from a tower and observes the angle of elevation of the top of the tower to be 60°. Find the height of the tower.
An observer point for ships moving in the sea 500m above the sea level. The person manning this point observes the angle of depression of twc boats as 45° and 30°. Find the distance between the boats when they are on the same side of the observation point and when they are on opposite sides of the observation point.
The angle of depression of a boat moving towards a diff is 30°. Three minutes later the angle of depression of the boat is 60°. Assuming that the boat is sailing at a uniform speed, determine the time it will take to reach the shore. Also, find the speed of the boat in m/second if the cliff is 450m high.
The angle of elevation of an aeroplane from a point on the ground is 45°. After 15 seconds, the angle of elevation changes to 30°. If the aeroplane is flying at a height of 3000 m, find the speed of the aeroplane.
An aeroplane is flying horizontally along a straight line at a height of 3000 m from the ground at a speed of 160 m/s. Find the time it would take for the angle of elevation of the plane as seen from a particular point on the ground to change from 60⁰ to 45⁰. Give your answer correct to the nearest second.
