Advertisements
Advertisements
प्रश्न
From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and the angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
उत्तर
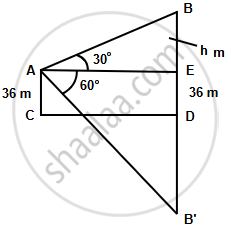
Let A be a point 36 m above the surface of the lake and B be the position of the bird. Let B' be the image if the brid in the water.
Here, AC = DE = 36 m, ∠BAE = 30° and ∠B’AE = 60°,
Let BE = h m,
Then, B'D = BD = 36 + h ...(∴ B’ is image of B about D)
∴ B’E = B’D + DE
= 36 + 36 + h
= 72 + h ...(i)
In ΔABE,
`(BE)/(AE) = tan 30^circ`
`=> AE = sqrt(3)h` ...(ii)
In ΔAB’E,
`(B^’E)/(AE) = tan 60^circ`
`=> (72 + h )/(AE) = sqrt(3)` ...[From (i)]
`=> 72 + h = (sqrt(3)h)sqrt(3)` ...[From (ii)]
`=>` 72 + h = 3h
∴ h = 36 m
Hence, the actual height of the bird above the surface of the lake = 36 + 36 = 72 m.
APPEARS IN
संबंधित प्रश्न
A bus covers a distance of 240 km at a uniform speed. Due to heavy rain, its speed gets reduced by 10 km/h and as such it takes two hrs longer to cover the total distance. Assuming the uniform speed to be ‘x’ km/h, form an equation and solve it to evaluate ‘x’.
Evaluate without using trigonometric tables.
`2((tan 35^@)/(cot 55^@))^2 + ((cot 55^@)/(tan 35^@)) - 3((sec 40^@)/(cosec 50^@))`
A man observes the angle of elevation of the top of a building to be 30o. He walks towards it in a horizontal line through its base. On covering 60 m the angle of elevation changes to 60o. Find the height of the building correct to the nearest metre.
A man stands 9 m away from a flag-pole. He observes that angle of elevation of the top of the pole is 28° and the angle of depression of the bottom of the pole is 13°. Calculate the height of the pole.
From the top of a cliff 92 m high, the angle of depression of a buoy is 20°. Calculate, to the nearest metre, the distance of the buoy from the foot of the cliff.
From the top of a light house 100 m high, the angles of depression of two ships are observed as 48° and 36° respectively. Find the distance between the two ships (in the nearest metre) if:
- the ships are on the same side of the light house,
- the ships are on the opposite sides of the light house.
The angles of depression and elevation of the top of a 12m high building from the top and the bottom of a tower are 60° and 30° respectively. Find the height of the tower, and its distance from the building.
The horizontal distance between two trees of different heights is 100m. The angle of depression of the top of the first tree when seen from the top of the second tree is 45°. If the height of the second tree is 150m, find the height of the first tree.
A man in a boat rowing away from a lighthouse 180 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° and 30°. Find the speed of the boat.
An aeroplane at an altitude of 250 m observes the angle of depression of two Boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
