Advertisements
Advertisements
प्रश्न
From the top of a cliff 92 m high, the angle of depression of a buoy is 20°. Calculate, to the nearest metre, the distance of the buoy from the foot of the cliff.
उत्तर
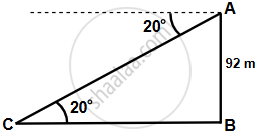
Let AB be the cliff and C be the buoy.
Given, AB = 92 m
Also, ∠ACB = 20°
∴`(AB)/(BC) = tan 20^circ`
`=> BC = 92/0.3640 = 252.7 m ≈ 253 m`
Hence, the buoy is at a distance of 253 m from the foot of the cliff.
APPEARS IN
संबंधित प्रश्न
A boy, 1.6 m tall, is 20 m away from a tower and observes the angle of elevation of the top of the tower to be (i) 45°, (ii) 60°. Find the height of the tower in each case.
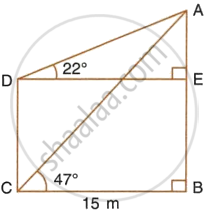
From the figure, given below, calculate the length of CD.
A person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 m away from the bank, he finds the angle of elevation to be 30°. Find:
- the height of the tree, correct to 2 decimal places,
- the width of the river.
An aeroplane, at an altitude of 250 m, observes the angles of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. If the boats are on the opposite sides of the aeroplane, find the width of the river. Write the answer correct to the nearest whole number.
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second is 30° and 24° respectively. Find the height of the two towers. Give your answers correct to 3 significant figures.

The length of the shadow of a statue increases by 8m, when the latitude of the sun changes from 45° to 30°. Calculate the height of the tower.
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be α, and β. If the height of the light house is 'h' m and the line joining the ships passes through the foot of the light house, show that the distance between the ship is `("h"(tan α + tan β))/(tanα tanβ)`m.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestone on opposite sides of the aeroplane are observed to be α, and β. Show that the height in miles of aeroplane above the road is `(tanα tanβ)/(tanα + tanβ)`.
From the top of a tower 60 m high, the angles of depression of the top and bottom of pole are observed to be 45° and 60° respectively. Find the height of the pole.

If the angle of elevation of a cloud from a point h meters above a lake is a*and the angle of depression of its reflection in the lake is |i. Prove that the height of the cloud is `(h (tan β + tan α))/(tan β - tan α)`.
