Advertisements
Advertisements
प्रश्न
A boy, 1.6 m tall, is 20 m away from a tower and observes the angle of elevation of the top of the tower to be (i) 45°, (ii) 60°. Find the height of the tower in each case.
उत्तर
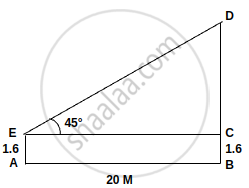
Let the height of the tower be h m.
i. Here, θ = 45°
∴ `tan 45^circ = (h - 1.6 )/20`
`=> 1 = (h - 1.6)/20`
∴ h = 21.6 m
So, height of the tower is 21.6 m
ii. Here θ = 60°
∴ `tan 60^circ = (h - 1.6)/20`
`=> sqrt(3) = (h - 1.6)/20`
∴ h = 20 × 1.732 + 1.6 = 36.24 m
So, height of the tower is 36.24 m.
APPEARS IN
संबंधित प्रश्न
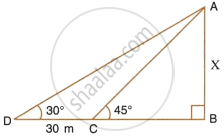
In the figure, given below, it is given that AB is perpandiculer to BD and is of length X metres. DC = 30 m, ∠ADB = 30° and ∠ACB = 45°. Without using tables, find X.
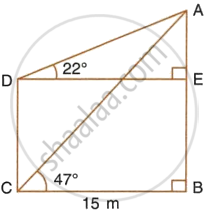
From the figure, given below, calculate the length of CD.
The length of the shadow of a tower standing on level plane is found to be 2y metres longer when the sun’s altitude is 30° than when it was 45°. Prove that the height of the tower is `y(sqrt(3) + 1)` metres.
Calculate AB.

In the given figure, from the top of a building AB = 60 m hight, the angle of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find:
- the horizontal distance between AB and CD.
- the height of the lamp post.
The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
A 10 m high pole is kept vertical by a steel wire. The wire is inclined at an angle of 40° with the horizontal ground. If the wire runs from the top of the pole to the point on the ground where Its other end is fixed, find the lenqth of the wire.
The height of an observation tower is 180m above sea level. A ship coming towards the tower is observed at an angle of depression of 30°. Calculate the distance of the boat from the foot of the observation tower.
In figures, find the length CF.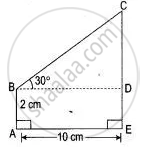
Two men on either side of a temple 75 m high observed the angle of elevation of the top of the temple to be 30° and 60° respectively. Find the distance between the two men.
