Advertisements
Advertisements
प्रश्न
The height of an observation tower is 180m above sea level. A ship coming towards the tower is observed at an angle of depression of 30°. Calculate the distance of the boat from the foot of the observation tower.
उत्तर
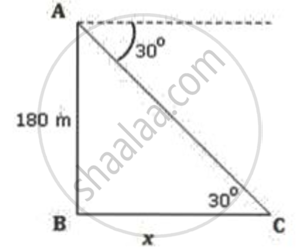
Let AB be the tower and C be the position of the ship.
Let the distance of the boat from the foot of the observation tower be x.
In triangle ABC,
tanθ = `"AB"/"BC"`
⇒ `tan 30^circ = 180/X`
⇒ `1/sqrt(3) = 180/X`
⇒ `X = 180sqrt(3) = 180 × 1.732 = 311.76`
Thus , the distance of the boat from the foot of the observation tower is 311.76 or 311.8 m.
APPEARS IN
संबंधित प्रश्न
The angle of elevation of the top of a tower, from a point on the ground and at a distance of 160 m from its foot, is found to be 60°. Find the height of the tower.
From the top of a cliff 92 m high, the angle of depression of a buoy is 20°. Calculate, to the nearest metre, the distance of the buoy from the foot of the cliff.
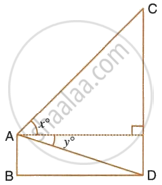
Find AD.

From a window A, 10 m above the ground the angle of elevation of the top C of a tower is x°, where tan `x^circ = 5/2` and the angle of depression of the foot D of the tower is y°, where tan `y^circ = 1/4`. Calculate the height CD of the tower in metres.
A man standing on the bank of a river observes that the angle of elevation of a tree on the opposite bank is 60°. When he moves 50 m away from the bank, he finds the angle of elevation to be 30°.
Calculate :
- the width of the river;
- the height of the tree.
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second is 30° and 24° respectively. Find the height of the two towers. Give your answers correct to 3 significant figures.

An aeroplane takes off at angle of `30^circ` with the ground . Find the height of the aeroplane above the ground when it has travelled 386m without changing direction .
A man on the deck of a ship is 10 m above water level. He observes that the angle of elevation of the top of a cliff is 42° and the angle of depression of the base is 20°. Calculate the distance of the cliff from the ship and the height of the cliff.
A man is standing on the deck of a ship, which is 10 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
An aeroplane at an altitude of 250 m observes the angle of depression of two Boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
