Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a tower, from a point on the ground and at a distance of 160 m from its foot, is found to be 60°. Find the height of the tower.
उत्तर
Let AB be the tower and C is the point which is 160 m away from the foot of the tower, i.e CB = 160 m
Let height of the tower be h
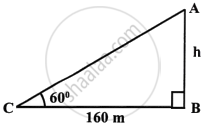
Now in right ΔABC, we have
`tan theta = (AB)/(BC)`
`=> tan 60^circ = h/160`
∴ h = 160 × tan 60°
= `160 xx sqrt(3) m`
= 160 × (1.732) m
= 277.12 m
∴ Required height of the tower = 277.12 m
APPEARS IN
संबंधित प्रश्न
The height of a tree is `sqrt(3)` times the length of its shadow. Find the angle of elevation of the sun.
Find the height of a building, when it is found that on walking towards it 40 m in a horizontal line through its base the angular elevation of its top changes from 30° to 45°.
The horizontal distance between two towers is 75 m and the angular depression of the top of the first tower as seen from the top of the second, which is 160 m high, is 45°. Find the height of the first tower.
As observed from the top of a 80 m tall lighthouse, the angles of depression of two ships, on the same side of a light house in a horizontal line with its base, are 30° and 40° respectively. Find the distance between the two ships. Give your answer corrected to the nearest metre.
Find the angle of depression from the top of a 140m high pillar of a milestone on the ground at a distance of 200m from the foot of the pillar.
A flagstaff stands on a vertical pole. The angles of elevation of the top and the bottom of the flagstaff from a point on the ground are found to be 60° and 30° respectively. If the height of the pole is 2.5m. Find the height of the flagstaff.
An observer, 1.5m tall, is 28.5m away from a tower 30m high. Determine the angle of elevation of the top of the tower from his eye.
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be α, and β. If the height of the light house is 'h' m and the line joining the ships passes through the foot of the light house, show that the distance between the ship is `("h"(tan α + tan β))/(tanα tanβ)`m.
With reference to the given figure, a man stands on the ground at point A, which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m. The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x°, where tan x° = `2/5`.
Calculate :
- the distance AB in metres;
- angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.
A pole being broken by the wind the top struck the ground at an angle of 30° and at a distance of 8m from the foot of the pole. Find the whole height of the pole.
