Advertisements
Advertisements
प्रश्न
As observed from the top of a 80 m tall lighthouse, the angles of depression of two ships, on the same side of a light house in a horizontal line with its base, are 30° and 40° respectively. Find the distance between the two ships. Give your answer corrected to the nearest metre.
उत्तर
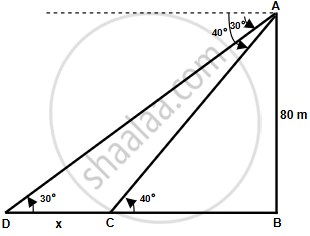
Let AB represent the lighthouse.
Let the two ships be at point D and C having angle of depression 30° and 40° respectively.
Let x be the distance between the two ships.
Clearly, m∠ACB = 40° and m∠ADB = 30°
In ΔACB
`tan 40^circ = 80/(CB)`
`=> CB = 80/ 0.84 = 95.24 m`
In ΔADB
`tan 30^circ = 80/(DB)`
`=> DB = 80/(0.58) = 137.93 m`
DC = DB – CB
`=>` x = 137.93 – 95.24
`=>` x = 42.69 ≈ 43 m
The distance between the two ship is 43 m.
संबंधित प्रश्न
In the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to 30o and 60o respectively. Find:
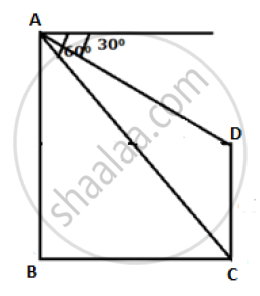
1) The horizontal distance between AB and CD.
2) The height of the lamp post.
Two persons are standing on the opposite sides of a tower. They observe the angles of elevation of the top of the tower to be 30° and 38° respectively. Find the distance between them, if the height of the tower is 50 m.
Two pillars of equal heights stand on either side of a roadway, which is 150 m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60° and 30°; find the height of the pillars and the position of the point.
A man on a cliff observes a boat, at an angle of depression 30°, which is sailing towards the shore to the point immediately beneath him. Three minutes later, the angle of depression of the boat is found to be 60°. Assuming that the boat sails at a uniform speed, determine:
- how much more time it will take to reach the shore?
- the speed of the boat in metre per second, if the height of the cliff is 500 m.
The length of the shadow of a tower standing on level plane is found to be 2y metres longer when the sun’s altitude is 30° than when it was 45°. Prove that the height of the tower is `y(sqrt(3) + 1)` metres.
The angles of elevation of the top of a tower from two points on the ground at distances a and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)` metre.
A vertical pole is 90m high and the length of its shadow is `90sqrt(3)`. what is the angle of elevation of the sun ?
An observer, 1.5m tall, is 28.5m away from a tower 30m high. Determine the angle of elevation of the top of the tower from his eye.
The angles of depression of two cars on a straight road as observed from the top of a 42m high building are 60° and 75° respectively. Find the distance between the cars if they are on opposite sides of the building.
The angle of elevation of an aeroplane from a point on the ground is 45°. After 15 seconds, the angle of elevation changes to 30°. If the aeroplane is flying at a height of 3000 m, find the speed of the aeroplane.
