Advertisements
Advertisements
प्रश्न
The angles of elevation of the top of a tower from two points on the ground at distances a and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)` metre.
उत्तर
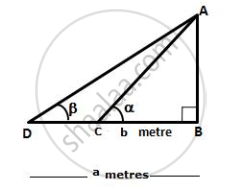
Let AB be the tower of height h metre
Let C and D be two points on the level ground such that BC = b metres, BD = a metres, ∠ACB = α and ∠ADB = β
Given, α + β = 90°
In ΔABC,
`(AB)/(BC) = tan alpha`
`=> h/b = tan alpha` ...(i)
In ΔABD,
`(AB)/(BD) = tan beta`
`=> h/a = tan (90^circ - alpha) = cot alpha` ...(ii)
Multiplying (i) by (ii), we get,
`(h/a)(h/b) = 1`
`=>` h2 = ab
∴ `h = sqrt(ab)` metre
Hence, height of the tower is `sqrt(ab)` metre.
APPEARS IN
संबंधित प्रश्न
The height of a tree is `sqrt(3)` times the length of its shadow. Find the angle of elevation of the sun.
The angle of elevation of the top of an unfinished tower from a point at a distance of 80 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
Find the height of a building, when it is found that on walking towards it 40 m in a horizontal line through its base the angular elevation of its top changes from 30° to 45°.
The horizontal distance between two towers is 75 m and the angular depression of the top of the first tower as seen from the top of the second, which is 160 m high, is 45°. Find the height of the first tower.
The length of the shadow of a tower standing on level plane is found to be 2y metres longer when the sun’s altitude is 30° than when it was 45°. Prove that the height of the tower is `y(sqrt(3) + 1)` metres.
A vertical tower stand on horizontel plane and is surmounted by a vertical flagstaff of height h metre. At a point on the plane, the angle of elevation of the bottom of the flagstaff is α and that of the top of flagstaff is β. Prove that the height of the tower is
`(h tan alpha)/(tan beta - tan alpha)`
A boy is 1.54 m tall. Standing at a distance of 3m in front of a 4.54 m high wall he can just manage to see the sun. Find the angle of elevation of the sun.
An observer point for ships moving in the sea 500m above the sea level. The person manning this point observes the angle of depression of twc boats as 45° and 30°. Find the distance between the boats when they are on the same side of the observation point and when they are on opposite sides of the observation point.
If the angle of elevation of a cloud from a point h meters above a lake is a*and the angle of depression of its reflection in the lake is |i. Prove that the height of the cloud is `(h (tan β + tan α))/(tan β - tan α)`.
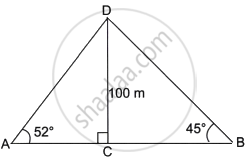
The angle of elevation of the top of a 100 m high tree from two points A and B on the opposite side of the tree are 52° and 45° respectively. Find the distance AB, to the nearest metre.