Advertisements
Advertisements
प्रश्न
The length of the shadow of a tower standing on level plane is found to be 2y metres longer when the sun’s altitude is 30° than when it was 45°. Prove that the height of the tower is `y(sqrt(3) + 1)` metres.
उत्तर
Let AB be the tower and AB = x
Distance CD = 2y
In right ΔADB, we have
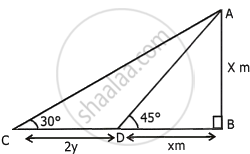
`tan theta = (AB)/(DB)`
`\implies tan 45^circ = x/(DB)`
`\implies 1 = x/(DB)`
`\implies` DB = x.
In right ΔACB, we have
`tan 30^circ = (AB)/(CB)`
`\implies 1/sqrt(3) = x/(CB)`
`\implies CB = sqrt(3)x`
`\implies x + 2y = sqrt(3)x`
∴ `sqrt(3)x - x = 2y`
`\implies x(sqrt(3) - 1) = 2y`
`x = (2y)/(sqrt(3) - 1)`
= `(2y(sqrt(3) + 1))/((sqrt(3) - 1)(sqrt(3) + 1))`
= `(2y(sqrt(3) + 1))/(3 - 1)`
= `(2y(sqrt(3) + 1))/2`
= `y(sqrt(3) + 1)`
∴ Required height of tower = `y(sqrt(3) + 1)`
APPEARS IN
संबंधित प्रश्न
Find the height of a tree when it is found that on walking away from it 20 m, in a horizontal line through its base, the elevation of its top changes from 60° to 30°.
The angle of elevation of the top of a tower is observed to be 60°. At a point, 30 m vertically above the first point of observation, the elevation is found to be 45°. Find:
- the height of the tower,
- its horizontal distance from the points of observation.
Calculate BC.
Find the angle of depression from the top of a 140m high pillar of a milestone on the ground at a distance of 200m from the foot of the pillar.
The height of an observation tower is 180m above sea level. A ship coming towards the tower is observed at an angle of depression of 30°. Calculate the distance of the boat from the foot of the observation tower.
A man on the top of a tower observes that a car is moving directly at a uniform speed towards it. If it takes 720 seconds for the angle of depression to change from 30° to 45°, how soon will the car reach the observation tower?
The angle of elevation of an aeroplane from a point on the ground is 45°. After 15 seconds, the angle of elevation changes to 30°. If the aeroplane is flying at a height of 3000 m, find the speed of the aeroplane.
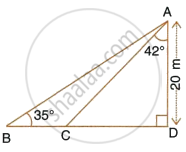
From the top of a lighthouse 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.
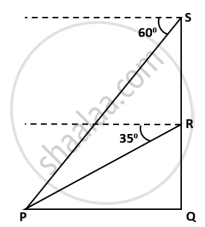
Two-person standing on the same side of a tower in a straight line with it measures the angle of elevation of the top of the tower as 25° and 50° respectively. If the height of the tower is 70 m find the distance between the two-person.
A drone camera is used to shoot an object P from two different positions R and S along the same vertical line QRS. The angle of depression of the object P from these two positions is 35° and 60° respectively as shown in the diagram. If the distance of the object P from point Q is 50 metres, then find the distance between R and S correct to the nearest meter.