Advertisements
Advertisements
प्रश्न
Find the height of a tree when it is found that on walking away from it 20 m, in a horizontal line through its base, the elevation of its top changes from 60° to 30°.
उत्तर
Let AB be the tree and its height be x
DC = 20 m.
Now in right ΔADB,
`tan theta = (AB)/(DB)`
`\implies tan 30^circ = x/(DB)`
`\implies 1/sqrt(3) = x/(DB)`
`\implies DB = sqrt(3)x`. ...(i)
In ΔACB, we have
`tan 60^circ = x/(CB)`
`\implies sqrt(3)/1 = x/(CB)`
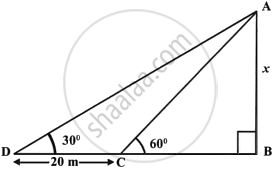
∴ `CB = x/sqrt(3) = (sqrt(3)x)/3` ...(ii)
But DB – CB = DC
`\implies sqrt(3)x - (sqrt(3)x)/3 = 20`
`\implies (3sqrt(3)x - sqrt(3)x)/3 = 20`
`\implies (2sqrt(3)x)/3 = 20`
`\implies x = (20 xx 3)/(2sqrt(3))`
= `(10 xx 3 xx sqrt(3))/(sqrt(3) xx sqrt(3))`
= `(30sqrt(3))/3`
∴ `x = 10sqrt(3)`
= 10 × (1.732)
= 17.32 m.
∴ Required height of the tree = 17.32 m
APPEARS IN
संबंधित प्रश्न
A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area.
A ladder is placed along a wall such that its upper end is resting against a vertical wall. The foot of the ladder is 2.4 m from the wall and the ladder is making an angle of 68° with the ground. Find the height, upto which the ladder reaches.
At a particular time, when the sun’s altitude is 30°, the length of the shadow of a vertical tower is 45 m. Calculate:
- the height of the tower.
- the length of the shadow of the same tower, when the sun’s altitude is:
- 45°
- 60°
The angle of elevation of the top of a tower is observed to be 60°. At a point, 30 m vertically above the first point of observation, the elevation is found to be 45°. Find:
- the height of the tower,
- its horizontal distance from the points of observation.
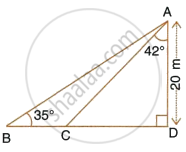
Calculate BC.
A man observes the angle of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m, the angle of elevation changes to 60°. Find the height of the building correct to the nearest metre.
The topmost branch of a tree is tied with a string attached to a pole in the ground. The length of this string Is 200m and it makes an angle of 45° with the ground. Find the distance of the pole to which the string is tied from the base of the tree.
The top of a palm tree having been broken by the wind struck the ground at an angle of 60° at a distance of 9m from the foot of the tree. Find the original height of the palm tree.
The angle of elevation of a tower from a point 200 m from its base is θ, when `tan θ = 2/5`. The angle of elevation of this tower from a point 120m from its base is `Φ`. Calculate the height of tower and the value of `Φ`.
The angle of depression of a boat moving towards a diff is 30°. Three minutes later the angle of depression of the boat is 60°. Assuming that the boat is sailing at a uniform speed, determine the time it will take to reach the shore. Also, find the speed of the boat in m/second if the cliff is 450m high.
