Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a tower is observed to be 60°. At a point, 30 m vertically above the first point of observation, the elevation is found to be 45°. Find:
- the height of the tower,
- its horizontal distance from the points of observation.
उत्तर
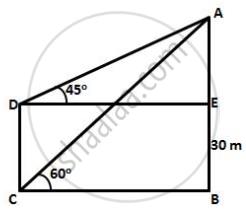
In ΔABC
`tan 60^circ = (h + 30)/x`
`xsqrt(3) = h + 30` ...(1)
In ΔADE
`tan 45^circ = h/x`
`1 = h/x`
h = x ...(2)
From equation (1)
`xsqrt(3) = x + 30`
`x(sqrt(3) - 1) = 30`
`x = 30/(sqrt(3) - 1) xx (sqrt(3) + 1)/(sqrt(3) + 1)`
`x = (30(sqrt(3) + 1))/(3 - 1)`
= `(30(1.732 + 1))/2`
= 15 × 2.732
= 40.980 m
From equation (2)
h = 40.98 m
Height of tower = h + 30
= 40.98 + 30
= 70.98 m
= 71 m (approx.)
Horizontal distance = x = 40.98 m = 41 m.
APPEARS IN
संबंधित प्रश्न
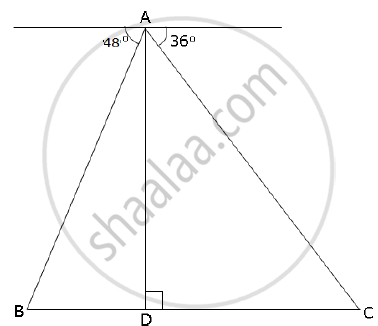
From the top of a lighthouse, 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.
Prove the following identities:
tan2 A – sin2 A = tan2 A . sin2 A
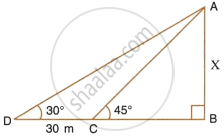
In the figure, given below, it is given that AB is perpandiculer to BD and is of length X metres. DC = 30 m, ∠ADB = 30° and ∠ACB = 45°. Without using tables, find X.
Find AD.

A vertical tower is 20 m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower?
A vertical tow er stands on a horizontal plane and is surmounted by a flagstaff of height 7m. From a point on the plane the angle of elevation of the bottom of the flagstaff is 30° and that of the top of the ft agstaff is 45°. Find the height of the tower.
From the top of a light house 96m high, the angles of depression of two ships in the river and at the same level as the base of the light house and on the same side of it, are α and β. If tan α = `1/4` and tan β = `1/7`, find the distance between the ships.
The horizontal distance between towers is 140 m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 30°. If the height of the second tower is 60m, find the height of the first tower.
The angle of depression of a boat moving towards a diff is 30°. Three minutes later the angle of depression of the boat is 60°. Assuming that the boat is sailing at a uniform speed, determine the time it will take to reach the shore. Also, find the speed of the boat in m/second if the cliff is 450m high.
A vertical tower standing on a horizontal plane is surmounted by a vertical flagstaff. At a point 100 m away from the foot of the tower, the angle of elevation of the top and bottom of the flagstaff are 54° and 42° respectively. Find the height of the flagstaff. Give your answer correct to nearest metre.

