Advertisements
Advertisements
प्रश्न
A vertical tow er stands on a horizontal plane and is surmounted by a flagstaff of height 7m. From a point on the plane the angle of elevation of the bottom of the flagstaff is 30° and that of the top of the ft agstaff is 45°. Find the height of the tower.
उत्तर
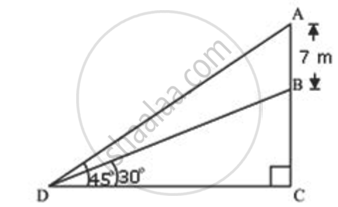
Let AB be the flagstaff, BC be the tower and D be the point on ground from where elevation angles are measured.
In ΔBCD
`"BC"/"CD" = tan 30^circ`
`"BC"/"CD" = 1/sqrt(3)`
`sqrt(3)"BC" = "CD"`
In ΔACD
`("AB + BC")/"CD" = tan 45^circ`
`("AB + BC")/(sqrt(3)"BC") = 1`
`7 + "BC" = sqrt(3)"BC"`
`"BC"(sqrt(3)-1) = 7`
BC = `((7)(sqrt(3) + 1))/((sqrt(3) - 1)(sqrt(3) + 1)`
= `(7(sqrt(3)+ 1))/((sqrt(3))^2 - (1)^2)`
= `(7(sqrt(3) + 1))/2 = 3.5(sqrt(3) + 1) = 3.5 xx 2.732 = 9.562`
Thus , the height of the tower is 9.562 m = 9.56 m.
APPEARS IN
संबंधित प्रश्न
An aeroplane at an altitude of 1500 metres, finds that two ships are sailing towards it in the same direction. The angles of depression as observed from the aeroplane are 45° and 30° respectively. Find the distance between the two ships
Prove the following identities:
tan2 A – sin2 A = tan2 A . sin2 A
A man on a cliff observes a boat, at an angle of depression 30°, which is sailing towards the shore to the point immediately beneath him. Three minutes later, the angle of depression of the boat is found to be 60°. Assuming that the boat sails at a uniform speed, determine:
- how much more time it will take to reach the shore?
- the speed of the boat in metre per second, if the height of the cliff is 500 m.
The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
Find the length of the shadow cast by a tree 60 m high when the sun's altitude is `30^circ`.
The topmost branch of a tree is tied with a string attached to a pole in the ground. The length of this string Is 200m and it makes an angle of 45° with the ground. Find the distance of the pole to which the string is tied from the base of the tree.
The horizontal distance between towers is 140 m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 30°. If the height of the second tower is 60m, find the height of the first tower.
A parachutist is descending vertically and makes angles of elevation of 45° and 60° from two observing points 100 m apart to his right. Find the height from which he falls and the distance of the point where he falls on the ground from the nearest observation pcint.
From the top of a tower 60 m high, the angles of depression of the top and bottom of pole are observed to be 45° and 60° respectively. Find the height of the pole.

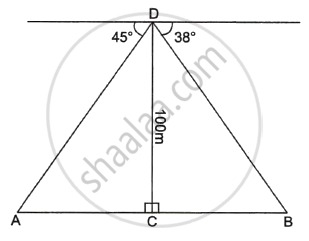
From the top of a tower 100 m high a man observes the angles of depression of two ships A and B, on opposite sides of the tower as 45° and 38° respectively. If the foot of the tower and the ships are in the same horizontal line find the distance between the two ships A and B to the nearest metre.
(Use Mathematical Tabels for this question)