Advertisements
Advertisements
प्रश्न
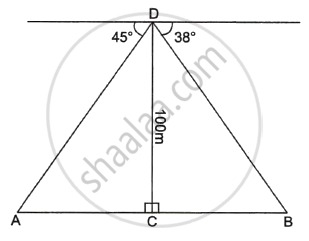
From the top of a tower 100 m high a man observes the angles of depression of two ships A and B, on opposite sides of the tower as 45° and 38° respectively. If the foot of the tower and the ships are in the same horizontal line find the distance between the two ships A and B to the nearest metre.
(Use Mathematical Tabels for this question)
उत्तर
Let AC = x,
BC = y
Now ∠A = 45° ...(Alternative angles)
and ∠B = 38° ...(Alternative angles)
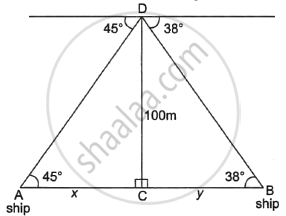
In ΔACD,
tan 45° = `100/x`
`\implies` 1 = `100/x`
∴ x = 100 ...(1)
In ΔBCD,
tan 38° = `100/y`
0.7812 = `100/y`
y = `100/0.7812 ≈ 128`
Hence Distance between two ships A, B
= x + y
= 100 + 128
= 228 m
APPEARS IN
संबंधित प्रश्न
Prove the following identities:
sin4A – cos4A = 2sin2A – 1
Prove the following identities:
tan2 A – sin2 A = tan2 A . sin2 A
A kite is attached to a string. Find the length of the string, when the height of the kite is 60 m and the string makes an angle 30° with the ground.
From the top of a cliff 92 m high, the angle of depression of a buoy is 20°. Calculate, to the nearest metre, the distance of the buoy from the foot of the cliff.
As observed from the top of a 80 m tall lighthouse, the angles of depression of two ships, on the same side of a light house in a horizontal line with its base, are 30° and 40° respectively. Find the distance between the two ships. Give your answer corrected to the nearest metre.
An aeroplane when flying at a height of 4km from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the aeroplanes at that instant.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7 meters. At a point in a plane, the angle of elevation of the bottom and the top of the flagstaff are respectively 30° and 60°. Find the height of the tower.
Two men on either side of a temple 75 m high observed the angle of elevation of the top of the temple to be 30° and 60° respectively. Find the distance between the two men.
Two-person standing on the same side of a tower in a straight line with it measures the angle of elevation of the top of the tower as 25° and 50° respectively. If the height of the tower is 70 m find the distance between the two-person.
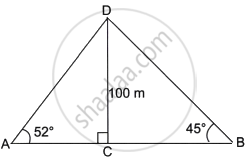
The angle of elevation of the top of a 100 m high tree from two points A and B on the opposite side of the tree are 52° and 45° respectively. Find the distance AB, to the nearest metre.