Advertisements
Advertisements
प्रश्न
A vertical tow er stands on a horizontal plane and is surmounted by a flagstaff of height 7m. From a point on the plane the angle of elevation of the bottom of the flagstaff is 30° and that of the top of the ft agstaff is 45°. Find the height of the tower.
उत्तर
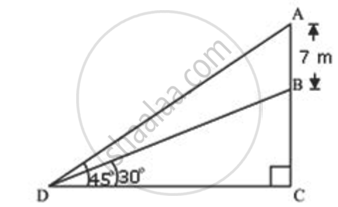
Let AB be the flagstaff, BC be the tower and D be the point on ground from where elevation angles are measured.
In ΔBCD
`"BC"/"CD" = tan 30^circ`
`"BC"/"CD" = 1/sqrt(3)`
`sqrt(3)"BC" = "CD"`
In ΔACD
`("AB + BC")/"CD" = tan 45^circ`
`("AB + BC")/(sqrt(3)"BC") = 1`
`7 + "BC" = sqrt(3)"BC"`
`"BC"(sqrt(3)-1) = 7`
BC = `((7)(sqrt(3) + 1))/((sqrt(3) - 1)(sqrt(3) + 1)`
= `(7(sqrt(3)+ 1))/((sqrt(3))^2 - (1)^2)`
= `(7(sqrt(3) + 1))/2 = 3.5(sqrt(3) + 1) = 3.5 xx 2.732 = 9.562`
Thus , the height of the tower is 9.562 m = 9.56 m.
APPEARS IN
संबंधित प्रश्न
An aeroplane at an altitude of 1500 metres, finds that two ships are sailing towards it in the same direction. The angles of depression as observed from the aeroplane are 45° and 30° respectively. Find the distance between the two ships
Two persons are standing on the opposite sides of a tower. They observe the angles of elevation of the top of the tower to be 30° and 38° respectively. Find the distance between them, if the height of the tower is 50 m.
The angles of elevation of the top of a tower from two points on the ground at distances a and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)` metre.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60° and the angle of depression of the bottom of the tower is 30°. Find:
- the height of the tower, if the height of the pole is 20 m;
- the height of the pole, if the height of the tower is 75 m.
The angle of elevation of the top of a vertical cliff from a point 30 m away from the foot of the cliff is 60°. Find the height of the cliff.
A kite tied to a string makes an angle of 60° with the ground. Find the perpendicular height of the kite if the length of its string is 250 m.
The top of a palm tree having been broken by the wind struck the ground at an angle of 60° at a distance of 9m from the foot of the tree. Find the original height of the palm tree.
The angle of elevation of the top of an unfinished tower at a point 150 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
If the angle of elevation of a cloud from a point h m above a lake is α, and the angle of depression of its reflection in the lake be β, prove that distance of the cloud from the point of observation is `("2h"secα)/(tanα - tanβ)`.
A man on the top of vertical observation tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower? (Give your answer correct to nearest seconds).
