Advertisements
Advertisements
प्रश्न
A man on the top of vertical observation tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower? (Give your answer correct to nearest seconds).
उत्तर
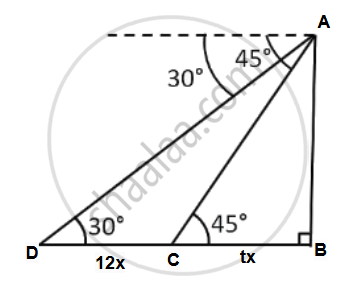
Here, ∠ACB = 30° and ∠ADB = 45°.
Let C denote the initial position of the car and D be its position after 12 minutes.
Let the speed of the car be x meter/minute, then
CD = 12x meters .....( ∵ Distance = speed x Time)
Let the car take t minutes to reach the tower from D.
Then, DB = tx meters
Now in the right-angled triangles ACB,
tan 30° = `"AB"/"BD"`
⇒ `1/sqrt3 = "AB"/("BC" + "CD")`
⇒ `1/sqrt3 = "AB"/(12x + tx)`
⇒ `"AB" = (12x + tx)/sqrt3` ....(1)
Also, in the right-angled triangle ADB,
tan 45° = `"AB"/"DB"`
⇒ 1 = `"AB"/"DB"`
⇒ AB = DB = tx ......(2)
From (1) and (2), we have
t = `12/(sqrt3 - 1) = 12(sqrt3 + 1)/2`
t = `6(sqrt3 + 1)`
t = 15.39
∴ Time = 16.39 minutes
Time = 16 minutes 23 seconds.
APPEARS IN
संबंधित प्रश्न
A vertical tower is 20 m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower?
As observed from the top of a 80 m tall lighthouse, the angles of depression of two ships, on the same side of a light house in a horizontal line with its base, are 30° and 40° respectively. Find the distance between the two ships. Give your answer corrected to the nearest metre.
The angle of elevation of the top of an unfinished tower at a point 150 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
A 1.4m tall boy stands at a point 50m away from a tower and observes the angle of elevation of the top of the tower to be 60°. Find the height of the tower.
A boy is standing on the ground and flying a kite with 100m of sting at an elevation of 30°. Another boy is standing on the roof of a 10m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
The angle of depression of a boat moving towards a diff is 30°. Three minutes later the angle of depression of the boat is 60°. Assuming that the boat is sailing at a uniform speed, determine the time it will take to reach the shore. Also, find the speed of the boat in m/second if the cliff is 450m high.
A ladder rests against a wall at an angle a, to the horizontal. Its foot is pulled away from the wall through a distance 'a', so that it slides a distance 'b' down the wall making an angle β with the horizontal. Show that `"a"/"b" = (cosα - cosβ)/(sinβ - sinα).`
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7 meters. At a point in a plane, the angle of elevation of the bottom and the top of the flagstaff are respectively 30° and 60°. Find the height of the tower.
Two-person standing on the same side of a tower in a straight line with it measures the angle of elevation of the top of the tower as 25° and 50° respectively. If the height of the tower is 70 m find the distance between the two-person.
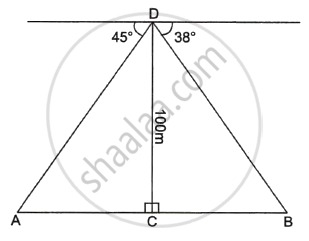
From the top of a tower 100 m high a man observes the angles of depression of two ships A and B, on opposite sides of the tower as 45° and 38° respectively. If the foot of the tower and the ships are in the same horizontal line find the distance between the two ships A and B to the nearest metre.
(Use Mathematical Tabels for this question)