Advertisements
Advertisements
प्रश्न
A ladder rests against a wall at an angle a, to the horizontal. Its foot is pulled away from the wall through a distance 'a', so that it slides a distance 'b' down the wall making an angle β with the horizontal. Show that `"a"/"b" = (cosα - cosβ)/(sinβ - sinα).`
उत्तर
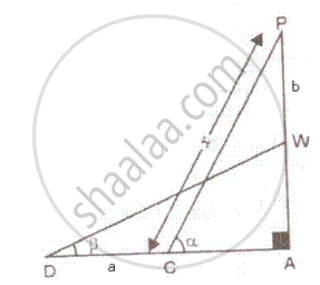
Let CP and DW be the two position of the ladder such that CP = DW = x (say).
CD = a , PW = b, ∠ACP = α and ∠ADW = β
In ΔAPC,
`"AC"/"CP" = cos α ⇒ "AC" = "x" cosα"` ....(i)
In ΔADW,
`"AD"/"DW" = cos β ⇒ ("AC + CD")/("DW") = cos β`
⇒ `("x" cosα + a)/"x" = cos β` [using (i)]
⇒ `"x" = a/(cos β - cos α)` ...(ii)
Again in ΔAPC, `"AP"/"CP" = sin α`
⇒ `"AP" = "x" sin α = (a sinα)/((cos β - cosα))` ....(iii) [Using (ii)]
Again in ΔADW, `"AW"/"DW" = sin β`
⇒ `"AW" = "x" sin β = (a sin β)/((cos β - cos α))` ...(iv)
Now , PW = AP - AW
⇒ `"b" = ((asinα)/(cosβ -cosα)) - ((asinβ)/(cosβ - cosα)) = (a(sinα -sinβ))/((cosβ - cosα))`
⇒ `a/b = (cosβ - cosα)/(sinα -sinβ)`
Hence proved.
APPEARS IN
संबंधित प्रश्न
Find the height of a building, when it is found that on walking towards it 40 m in a horizontal line through its base the angular elevation of its top changes from 30° to 45°.
The angle of elevation of the top of a tower is observed to be 60°. At a point, 30 m vertically above the first point of observation, the elevation is found to be 45°. Find:
- the height of the tower,
- its horizontal distance from the points of observation.
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
A vertical tower stand on horizontel plane and is surmounted by a vertical flagstaff of height h metre. At a point on the plane, the angle of elevation of the bottom of the flagstaff is α and that of the top of flagstaff is β. Prove that the height of the tower is
`(h tan alpha)/(tan beta - tan alpha)`
The angles of elevation of the top of a tower from two points on the ground at distances a and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)` metre.
The angles of depression and elevation of the top of a 12m high building from the top and the bottom of a tower are 60° and 30° respectively. Find the height of the tower, and its distance from the building.
The angle of elevation of a stationary cloud from a point 25m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. What is the height of the cloud above the lake-level?
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60o and the angle of depression of the bottom of the tower is 30o. Find: the height of the pole, if the height of the tower is 75 m.
A round balloon of radius 'a' subtends an angle θ at the eye of the observer while the angle of elevation of its centre is Φ. Prove that the height of the centre of the balloon is a sin Φ cosec `θ/2`.
An aeroplane is flying horizontally along a straight line at a height of 3000 m from the ground at a speed of 160 m/s. Find the time it would take for the angle of elevation of the plane as seen from a particular point on the ground to change from 60⁰ to 45⁰. Give your answer correct to the nearest second.
