Advertisements
Advertisements
प्रश्न
A ladder rests against a wall at an angle a, to the horizontal. Its foot is pulled away from the wall through a distance 'a', so that it slides a distance 'b' down the wall making an angle β with the horizontal. Show that `"a"/"b" = (cosα - cosβ)/(sinβ - sinα).`
उत्तर
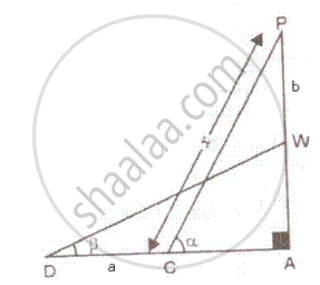
Let CP and DW be the two position of the ladder such that CP = DW = x (say).
CD = a , PW = b, ∠ACP = α and ∠ADW = β
In ΔAPC,
`"AC"/"CP" = cos α ⇒ "AC" = "x" cosα"` ....(i)
In ΔADW,
`"AD"/"DW" = cos β ⇒ ("AC + CD")/("DW") = cos β`
⇒ `("x" cosα + a)/"x" = cos β` [using (i)]
⇒ `"x" = a/(cos β - cos α)` ...(ii)
Again in ΔAPC, `"AP"/"CP" = sin α`
⇒ `"AP" = "x" sin α = (a sinα)/((cos β - cosα))` ....(iii) [Using (ii)]
Again in ΔADW, `"AW"/"DW" = sin β`
⇒ `"AW" = "x" sin β = (a sin β)/((cos β - cos α))` ...(iv)
Now , PW = AP - AW
⇒ `"b" = ((asinα)/(cosβ -cosα)) - ((asinβ)/(cosβ - cosα)) = (a(sinα -sinβ))/((cosβ - cosα))`
⇒ `a/b = (cosβ - cosα)/(sinα -sinβ)`
Hence proved.
APPEARS IN
संबंधित प्रश्न
An aeroplane at an altitude of 1500 metres, finds that two ships are sailing towards it in the same direction. The angles of depression as observed from the aeroplane are 45° and 30° respectively. Find the distance between the two ships
A man observes the angle of elevation of the top of the tower to be 45°. He walks towards it in a horizontal line through its base. On covering 20 m the angle of elevation changes to 60°. Find the height of the tower correct to 2 significant figures.
The height of an observation tower is 180m above sea level. A ship coming towards the tower is observed at an angle of depression of 30°. Calculate the distance of the boat from the foot of the observation tower.
A boy is 1.54 m tall. Standing at a distance of 3m in front of a 4.54 m high wall he can just manage to see the sun. Find the angle of elevation of the sun.
Two persons standing on opposite sides of a tower observe the angles of elevation of the top of the tower to be 60° and 50° respectively. Find the distance between them, if the height of the tower is 80m.
The angle of elevation of a stationary cloud from a point 25m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. What is the height of the cloud above the lake-level?
With reference to the given figure, a man stands on the ground at point A, which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m. The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x°, where tan x° = `2/5`.
Calculate :
- the distance AB in metres;
- angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60o and the angle of depression of the bottom of the tower is 30o. Find: the height of the pole, if the height of the tower is 75 m.
In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

An aeroplane when 3,000 meters high passes vertically above another aeroplane at an instance when their angles of elevation at the same observation point are 60° and 45° respectively. How many meters higher is the one than the other?
