Advertisements
Advertisements
प्रश्न
An aeroplane when 3,000 meters high passes vertically above another aeroplane at an instance when their angles of elevation at the same observation point are 60° and 45° respectively. How many meters higher is the one than the other?
उत्तर
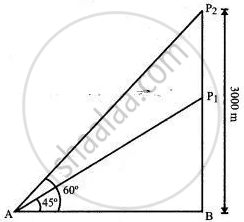
Let P1 and P2 denote the positions of the two planes. Then in right-angled ΔP1AB,
`(P_1B)/(AB) = tan 45° ⇒ P_1B = AB`
In right-angled ΔP2AB,
⇒ `(P_2B)/AB = tan 60° = sqrt3`
⇒ AB = `(P_2B)/sqrt3`
⇒ AB = `3000/sqrt3`
⇒ AB = 1000√3
∴ Vertical distance between the two planes is P1P2 = P2B - P1B
= 3000 - 1000√3
= 1000( 3 - √3) m
APPEARS IN
संबंधित प्रश्न
A bus covers a distance of 240 km at a uniform speed. Due to heavy rain, its speed gets reduced by 10 km/h and as such it takes two hrs longer to cover the total distance. Assuming the uniform speed to be ‘x’ km/h, form an equation and solve it to evaluate ‘x’.
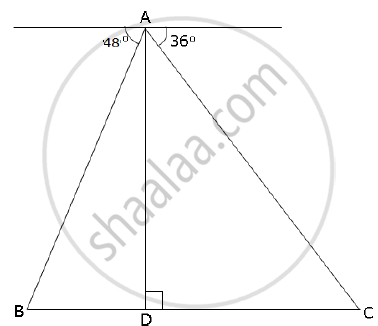
From the top of a lighthouse, 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.
A ladder is placed along a wall such that its upper end is resting against a vertical wall. The foot of the ladder is 2.4 m from the wall and the ladder is making an angle of 68° with the ground. Find the height, upto which the ladder reaches.
Two pillars of equal heights stand on either side of a roadway, which is 150 m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60° and 30°; find the height of the pillars and the position of the point.
A man observes the angle of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m, the angle of elevation changes to 60°. Find the height of the building correct to the nearest metre.
The top of a palm tree having been broken by the wind struck the ground at an angle of 60° at a distance of 9m from the foot of the tree. Find the original height of the palm tree.
The angle of elevation of a tower from a point 200 m from its base is θ, when `tan θ = 2/5`. The angle of elevation of this tower from a point 120m from its base is `Φ`. Calculate the height of tower and the value of `Φ`.
Of the two trees are on either side of a river, one of them is 50m high. From the top of this tree the angles of depression of the top and the foot of the other tree are 30° and 60° respectively. Find the width of the river and the height of the other tree.
The angle of elevation of a tower from a point in line with its base is `45^circ` . On moving 20m towards the tower , the angle of elevation changes to `60^circ` . Find the height of the tower.
In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

