Advertisements
Advertisements
प्रश्न
An aeroplane when 3,000 meters high passes vertically above another aeroplane at an instance when their angles of elevation at the same observation point are 60° and 45° respectively. How many meters higher is the one than the other?
उत्तर
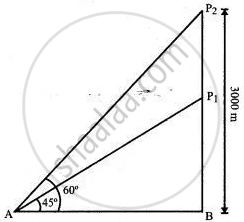
Let P1 and P2 denote the positions of the two planes. Then in right-angled ΔP1AB,
`(P_1B)/(AB) = tan 45° ⇒ P_1B = AB`
In right-angled ΔP2AB,
⇒ `(P_2B)/AB = tan 60° = sqrt3`
⇒ AB = `(P_2B)/sqrt3`
⇒ AB = `3000/sqrt3`
⇒ AB = 1000√3
∴ Vertical distance between the two planes is P1P2 = P2B - P1B
= 3000 - 1000√3
= 1000( 3 - √3) m
APPEARS IN
संबंधित प्रश्न
A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area.
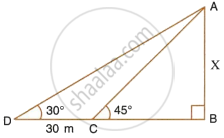
In the figure, given below, it is given that AB is perpandiculer to BD and is of length X metres. DC = 30 m, ∠ADB = 30° and ∠ACB = 45°. Without using tables, find X.
A man on a cliff observes a boat, at an angle of depression 30°, which is sailing towards the shore to the point immediately beneath him. Three minutes later, the angle of depression of the boat is found to be 60°. Assuming that the boat sails at a uniform speed, determine:
- how much more time it will take to reach the shore?
- the speed of the boat in metre per second, if the height of the cliff is 500 m.
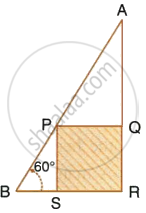
In the following diagram, AB is a floor-board; PQRS is a cubical box with each edge = 1 m and ∠B = 60°. Calculate the length of the board AB.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60° and the angle of depression of the bottom of the tower is 30°. Find:
- the height of the tower, if the height of the pole is 20 m;
- the height of the pole, if the height of the tower is 75 m.
An aeroplane at an altitude of 200 m observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river.
From the top of a light house 96m high, the angles of depression of two ships in the river and at the same level as the base of the light house and on the same side of it, are α and β. If tan α = `1/4` and tan β = `1/7`, find the distance between the ships.
The angle of depression of a boat moving towards a diff is 30°. Three minutes later the angle of depression of the boat is 60°. Assuming that the boat is sailing at a uniform speed, determine the time it will take to reach the shore. Also, find the speed of the boat in m/second if the cliff is 450m high.
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40m vertically above X, the angle of elevation is 45°. Find the height of the tower PQ and the distance XQ.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestone on opposite sides of the aeroplane are observed to be α, and β. Show that the height in miles of aeroplane above the road is `(tanα tanβ)/(tanα + tanβ)`.
