Advertisements
Advertisements
प्रश्न
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40m vertically above X, the angle of elevation is 45°. Find the height of the tower PQ and the distance XQ.
उत्तर
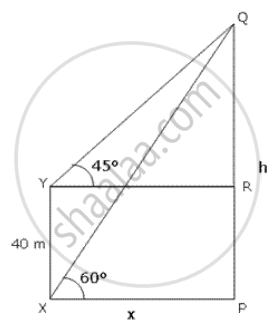
In the figure, PQ is the tower.
In ΔPQX,
∴ `"h"/"x" = tan60^circ = sqrt(3)`
⇒ h = `sqrt(3)`x ...(1)
In ΔQRY,
`("h" - 40)/"x" = tan 45^circ = 1`
⇒ h = 40 + x ...(2)
From (1) and (2),
`sqrt(3)`x = 40 + x
⇒ `(sqrt(3) - 1)"x" = 40`
⇒ `"x" = 40/(sqrt(3) - 1) = (40(sqrt(3) + 1))/((sqrt(3) - 1)(sqrt(3) + 1)) = 40/2(sqrt(3) + 1) = 20(sqrt(3) + 1)`
∴ `"h" = 40 + 20(sqrt(3) + 1) = 20sqrt(3) + 60 = 20(sqrt(3) + 3) = 20 xx 4.732 = 94.64`
Thus , the height of the tower PQ is 94.64 m.
Again, in ΔPQX,
∴ `"h"/"XQ" = sin60^circ = 1/sqrt(2)`
⇒ `"XQ" = sqrt(2)"h" = 1.414 xx 94.64 = 109.3`m
Thus , the distance XQ is 109.3m.
APPEARS IN
संबंधित प्रश्न
An aeroplane at an altitude of 1500 metres, finds that two ships are sailing towards it in the same direction. The angles of depression as observed from the aeroplane are 45° and 30° respectively. Find the distance between the two ships
At a particular time, when the sun’s altitude is 30°, the length of the shadow of a vertical tower is 45 m. Calculate:
- the height of the tower.
- the length of the shadow of the same tower, when the sun’s altitude is:
- 45°
- 60°
The distance of the gate of a temple from its base is `sqrt(3)` times it height. Find the angle of elevation of the top of the temple.
The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
A kite tied to a string makes an angle of 60° with the ground. Find the perpendicular height of the kite if the length of its string is 250 m.
A ladder rests against a tree on one side of a street. The foot of the ladder makes an angle of 50° with the ground. When the ladder is turned over to rest against another tree on the other side of the street it makes an angle of 40° with the ground. If the length of the ladder is 60m, find the width of the street.
The angle of elevation of a cloud from a point 60m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
A ladder rests against a wall at an angle a, to the horizontal. Its foot is pulled away from the wall through a distance 'a', so that it slides a distance 'b' down the wall making an angle β with the horizontal. Show that `"a"/"b" = (cosα - cosβ)/(sinβ - sinα).`
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60o and the angle of depression of the bottom of the tower is 30o. Find: the height of the pole, if the height of the tower is 75 m.
From the top of a tower 60 m high, the angles of depression of the top and bottom of pole are observed to be 45° and 60° respectively. Find the height of the pole.

