Advertisements
Advertisements
प्रश्न
The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
उत्तर
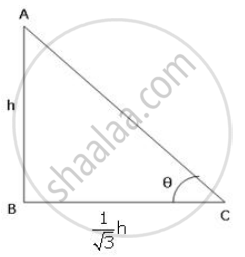
Let AB be the pillar and BC be its shadow.
Let h be the height of the pillar . Then,
BC = `1/sqrt(3)`h
In ΔABC,
tanθ = `"AB"/"BC"`
⇒ `tanθ = h/(h/sqrt(3)) = sqrt(3)`
But , `tan60^circ = sqrt(3)`
∴ `θ = 60^circ`
APPEARS IN
संबंधित प्रश्न
The angle of elevation from a point P of the top of a tower QR, 50 m high is 60o and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre

Two vertical poles are on either side of a road. A 30 m long ladder is placed between the two poles. When the ladder rests against one pole, it makes angle 32°24′ with the pole and when it is turned to rest against another pole, it makes angle 32°24′ with the road. Calculate the width of the road.
Find AD.

A vertical pole is 90m high and the length of its shadow is `90sqrt(3)`. what is the angle of elevation of the sun ?
The topmost branch of a tree is tied with a string attached to a pole in the ground. The length of this string Is 200m and it makes an angle of 45° with the ground. Find the distance of the pole to which the string is tied from the base of the tree.
The angle of elevation of a cloud from a point 60m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
A man on the top of a tower observes a truck at an angle of depression ∝ where `∝ = 1/sqrt(5)` and sees that it is moving towards the base of the tower. Ten minutes later, the angle of depression of the truck is found to `β = sqrt(5)`. Assuming that the truck moves at a uniform speed, determine how much more ti me it will take to each the base of the tower?
Two men on either side of a temple 75 m high observed the angle of elevation of the top of the temple to be 30° and 60° respectively. Find the distance between the two men.
If the angle of elevation of a cloud from a point h meters above a lake is a*and the angle of depression of its reflection in the lake is |i. Prove that the height of the cloud is `(h (tan β + tan α))/(tan β - tan α)`.
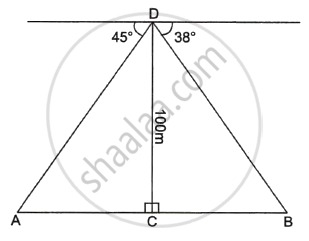
From the top of a tower 100 m high a man observes the angles of depression of two ships A and B, on opposite sides of the tower as 45° and 38° respectively. If the foot of the tower and the ships are in the same horizontal line find the distance between the two ships A and B to the nearest metre.
(Use Mathematical Tabels for this question)