Advertisements
Advertisements
प्रश्न
A man on the top of a tower observes a truck at an angle of depression ∝ where `∝ = 1/sqrt(5)` and sees that it is moving towards the base of the tower. Ten minutes later, the angle of depression of the truck is found to `β = sqrt(5)`. Assuming that the truck moves at a uniform speed, determine how much more ti me it will take to each the base of the tower?
उत्तर
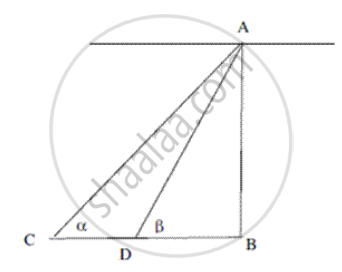
In the figure , AB is the tower . A is the position of the man. C and D are the two positions of the truck.
Let the speed of the truck be x m/sec
Distance CD = Speed × time = 600x
In right triangle ABC,
`tan α = "h"/"BC"`
It is a given that `tan α = 1/sqrt(5)`
`"BC" = "h"sqrt(5)` .. (1)
In right triangle ABD,
`tan β = "h"/"BD"`
It is given that `tan β = sqrt(5)`
`"h" = sqrt(5)"BD"`
Now , CD = BC - BD
600x = 5BD - BD
BD = 150x
Time taken = `(150"x")/"x"` = 150 seconds
Thus , the time taken by the truck to reach the tower is 150 sec = 2 min 30 sec.
APPEARS IN
संबंधित प्रश्न
The horizontal distance between two towers is 75 m and the angular depression of the top of the first tower as seen from the top of the second, which is 160 m high, is 45°. Find the height of the first tower.
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second is 30° and 24° respectively. Find the height of the two towers. Give your answers correct to 3 significant figures.

The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
A ladder rests against a tree on one side of a street. The foot of the ladder makes an angle of 50° with the ground. When the ladder is turned over to rest against another tree on the other side of the street it makes an angle of 40° with the ground. If the length of the ladder is 60m, find the width of the street.
The angle of elevation of the top of an unfinished tower at a point 150 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
A parachutist is descending vertically and makes angles of elevation of 45° and 60° from two observing points 100 m apart to his right. Find the height from which he falls and the distance of the point where he falls on the ground from the nearest observation pcint.
If the angle of elevation of a cloud from a point h m above a lake is α, and the angle of depression of its reflection in the lake be β, prove that distance of the cloud from the point of observation is `("2h"secα)/(tanα - tanβ)`.
The string of a kite is 150 m long and it makes an angle of 60° with the horizontal. Find the height of the kite from the ground.
A round balloon of radius 'a' subtends an angle θ at the eye of the observer while the angle of elevation of its centre is Φ. Prove that the height of the centre of the balloon is a sin Φ cosec `θ/2`.
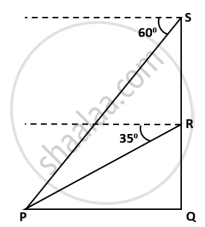
A drone camera is used to shoot an object P from two different positions R and S along the same vertical line QRS. The angle of depression of the object P from these two positions is 35° and 60° respectively as shown in the diagram. If the distance of the object P from point Q is 50 metres, then find the distance between R and S correct to the nearest meter.