Advertisements
Advertisements
प्रश्न
A man standing on a cliff observes a ship at an angle of depression of the ship is 30°, approaching the shore just beneath him. Three minutes later, the angle of depression of the ship is 60°. How soon will it reach the shore?
उत्तर
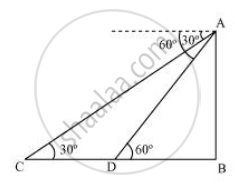
Let AB be the tower.
Initial position of ship is C , which changes to D after 3 minutes.
In ΔADB
`"AB"/"DB" = tan60^circ`
`"AB"/"DB" = sqrt(3)`
`"DB" = "AB"/sqrt(3)`
In ΔABC
`"AB"/"BC" = tan30^circ`
`"AB"/"BD + DC" = 1/sqrt(3)`
`"AB"sqrt(3) = "BD + DC"`
`"AB"sqrt(3) = "AB"/sqrt(3) + "DC"`
`"DC" = "AB"sqrt(3) - "AB"/sqrt(3) = "AB"(sqrt(3) - 1/sqrt(3))`
= `"2AB"/sqrt(3)`
Time taken by car to travel DC distance `("i.e". "2AB"/sqrt(3))` = 3 minutes
Time taken by car to travel DB distance `("i.e". "AB"/sqrt(3))`
= `3/((2AB)/sqrt(3)) xx "AB"/sqrt(3) = 3/2` = 1 min 30 secs
Thus , the total time taken is 3 minutes + 1 minute 30 seconds = 4 minutes 30 seconds.
APPEARS IN
संबंधित प्रश्न
The angle of elevation from a point P of the top of a tower QR, 50 m high is 60o and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre

An aeroplane at an altitude of 250 m observes the angle of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
Two pillars of equal heights stand on either side of a roadway, which is 150 m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60° and 30°; find the height of the pillars and the position of the point.
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
Calculate BC.
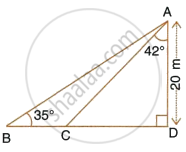
From the top of a light house 96m high, the angles of depression of two ships in the river and at the same level as the base of the light house and on the same side of it, are α and β. If tan α = `1/4` and tan β = `1/7`, find the distance between the ships.
Of the two trees are on either side of a river, one of them is 50m high. From the top of this tree the angles of depression of the top and the foot of the other tree are 30° and 60° respectively. Find the width of the river and the height of the other tree.
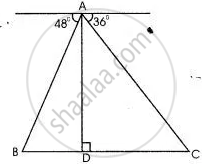
From the top of a lighthouse 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.
A pole being broken by the wind the top struck the ground at an angle of 30° and at a distance of 8m from the foot of the pole. Find the whole height of the pole.
From two points A and B on the same side of a building, the angles of elevation of the top of the building are 30° and 60° respectively. If the height of the building is 10 m, find the distance between A and B correct to two decimal places.
