Advertisements
Advertisements
प्रश्न
Of the two trees are on either side of a river, one of them is 50m high. From the top of this tree the angles of depression of the top and the foot of the other tree are 30° and 60° respectively. Find the width of the river and the height of the other tree.
उत्तर
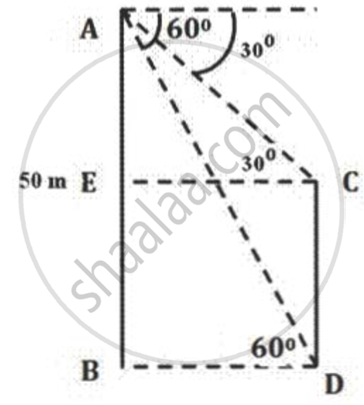
Let AB and CD be the two trees.
In ΔAEC,
`tan30^circ = "EA"/"EC"`
⇒ `1/sqrt(3) = "EA"/"EC"`
⇒ `"EC" = sqrt(3)"EA"` ....(1)
In ΔABD,
`tan60^circ = "AB"/"BD" = sqrt(3)`
⇒ `50/"BD" = sqrt(3)`
⇒ `"BD" = 50/sqrt(3)`
Thus , the width of the river is `"BD" = 50/sqrt(3) = 28.8` m.
From (1),
`"EA" = "EC"/sqrt(3) = "BD"/sqrt(3) = 50/3 = 16.67`
Height of the other tree =CD = 50 - EA= 50 - 16.67 = 33.33 m
APPEARS IN
संबंधित प्रश्न
A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area.
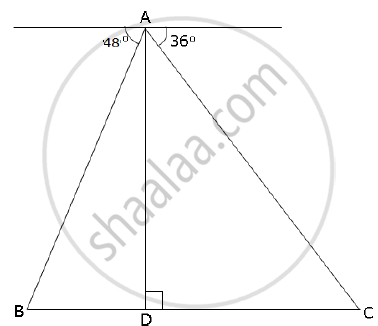
From the top of a lighthouse, 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.
The angle of elevation of the top of an unfinished tower from a point at a distance of 80 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
The length of the shadow of a tower standing on level plane is found to be 2y metres longer when the sun’s altitude is 30° than when it was 45°. Prove that the height of the tower is `y(sqrt(3) + 1)` metres.
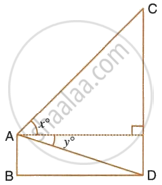
Find AD.

From a window A, 10 m above the ground the angle of elevation of the top C of a tower is x°, where tan `x^circ = 5/2` and the angle of depression of the foot D of the tower is y°, where tan `y^circ = 1/4`. Calculate the height CD of the tower in metres.
A vertical tow er stands on a horizontal plane and is surmounted by a flagstaff of height 7m. From a point on the plane the angle of elevation of the bottom of the flagstaff is 30° and that of the top of the ft agstaff is 45°. Find the height of the tower.
A boy is 1.54 m tall. Standing at a distance of 3m in front of a 4.54 m high wall he can just manage to see the sun. Find the angle of elevation of the sun.
A man in a boat rowing away from a lighthouse 180 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° and 30°. Find the speed of the boat.
From two points A and B on the same side of a building, the angles of elevation of the top of the building are 30° and 60° respectively. If the height of the building is 10 m, find the distance between A and B correct to two decimal places.
