Advertisements
Advertisements
प्रश्न
A man in a boat rowing away from a lighthouse 180 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° and 30°. Find the speed of the boat.
उत्तर
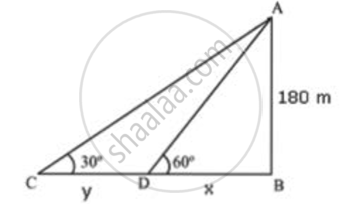
Let AB be the lighthouse.
Initial position of boat is C, which changes to D after 2 minutes.
In ΔADB
`"AB"/"DB" = tan60^circ`
`180/"x" = sqrt(3)`
`"x" = 180/sqrt(3)`
In ΔABC
`"AB"/"BC" = tan30^circ`
`180/("x + y") = 1/sqrt(3)`
`180sqrt(3) = "x + y"`
`180sqrt(3) = 180/sqrt(3) + "y"`
`"y" = 180(sqrt(3) - 1/sqrt(3)) = 180(2/sqrt(3)) = 360/sqrt(3)`
Time taken by car to travel DC distance `("i.e". 360/sqrt(3))` = 2 minutes = 120 seconds
Speed of the boat = `"Distance"/"Time" = (360/sqrt(3))/120 = 3/sqrt(3) = 3/sqrt(3) xx sqrt(3)/sqrt(3) = (3sqrt(3))/3 = sqrt(3) = 1.732`
Thus , the speed of the boat is 1.732 m/sec.
APPEARS IN
संबंधित प्रश्न
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the second tower is 30° and 24° respectively.
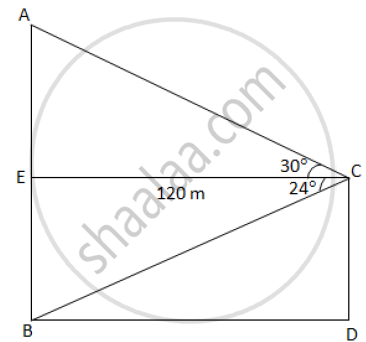
Find the height of the two towers. Give your answer correct to 3 significant figures
The angle of elevation of the top of an unfinished tower from a point at a distance of 80 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
Find AD.

A man observes the angle of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m, the angle of elevation changes to 60°. Find the height of the building correct to the nearest metre.
A vertical tow er stands on a horizontal plane and is surmounted by a flagstaff of height 7m. From a point on the plane the angle of elevation of the bottom of the flagstaff is 30° and that of the top of the ft agstaff is 45°. Find the height of the tower.
The angle of elevation of the top of an unfinished tower at a point 150 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
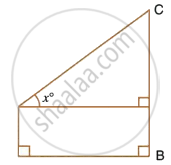
With reference to the given figure, a man stands on the ground at point A, which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m. The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x°, where tan x° = `2/5`.
Calculate :
- the distance AB in metres;
- angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.
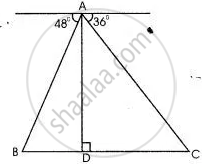
From the top of a lighthouse 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.
A pole being broken by the wind the top struck the ground at an angle of 30° and at a distance of 8m from the foot of the pole. Find the whole height of the pole.
