Advertisements
Advertisements
प्रश्न
A man observes the angle of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m, the angle of elevation changes to 60°. Find the height of the building correct to the nearest metre.
उत्तर
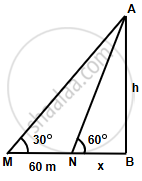
Let AB be a building and M and N are the two positions of the man which makes angle of elevation of top of buildings as 30° and 60° respectively.
MN = 60 m
Let AB = h and NB = x m
Now in right ΔAMB,
`tan 30^circ = (AB)/(MB)`
`=> tan 30^circ = h/(60 + x)`
`=> 1/sqrt(3) = h/(60 + x)`
`=> 60 + x = sqrt(3)h`
`=> x = sqrt(3)h - 60` ...(1)
Similarly in right ΔANB,
`tan 60^circ = (AB)/(NB)`
`tan 60^circ = h/(60 + x)`
`=> sqrt(3) = h/x`
`=> x = h/sqrt(3)` ...(2)
From (1) and (2), we have,
`sqrt(3)h - 60 = h/sqrt(3)`
`=> 3h - 60sqrt(3) = h`
`=> 3h - h = 60sqrt(3)`
`=> 2h = 60sqrt(3)`
`=> h= (60sqrt(3))/(2)`
`=> h = 30sqrt(3) = 30 xx 1.732`
`=>` h = 51.96 m
∴ Height of the building = 51.96 = 52 m (approx)
संबंधित प्रश्न
A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area.
A ladder is placed along a wall such that its upper end is resting against a vertical wall. The foot of the ladder is 2.4 m from the wall and the ladder is making an angle of 68° with the ground. Find the height, upto which the ladder reaches.
The angle of elevation of the top of an unfinished tower from a point at a distance of 80 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
An aeroplane, at an altitude of 250 m, observes the angles of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. If the boats are on the opposite sides of the aeroplane, find the width of the river. Write the answer correct to the nearest whole number.
The topmost branch of a tree is tied with a string attached to a pole in the ground. The length of this string Is 200m and it makes an angle of 45° with the ground. Find the distance of the pole to which the string is tied from the base of the tree.
From the top of a 60m high building the angles of depression of the top and bottom of a lamp post are 30° and 60° respectively. Find the distance on the ground between the building and the lamp post and the difference in their heights.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a diff is 45° and the angle of depression of the base is 30°. Find the distance of the diff from the ship and the height of the cliff.
Of the two trees are on either side of a river, one of them is 50m high. From the top of this tree the angles of depression of the top and the foot of the other tree are 30° and 60° respectively. Find the width of the river and the height of the other tree.
A ladder rests against a wall at an angle a, to the horizontal. Its foot is pulled away from the wall through a distance 'a', so that it slides a distance 'b' down the wall making an angle β with the horizontal. Show that `"a"/"b" = (cosα - cosβ)/(sinβ - sinα).`
An aeroplane is flying horizontally along a straight line at a height of 3000 m from the ground at a speed of 160 m/s. Find the time it would take for the angle of elevation of the plane as seen from a particular point on the ground to change from 60⁰ to 45⁰. Give your answer correct to the nearest second.
