Advertisements
Advertisements
Question
A man observes the angle of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m, the angle of elevation changes to 60°. Find the height of the building correct to the nearest metre.
Solution
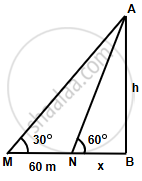
Let AB be a building and M and N are the two positions of the man which makes angle of elevation of top of buildings as 30° and 60° respectively.
MN = 60 m
Let AB = h and NB = x m
Now in right ΔAMB,
`tan 30^circ = (AB)/(MB)`
`=> tan 30^circ = h/(60 + x)`
`=> 1/sqrt(3) = h/(60 + x)`
`=> 60 + x = sqrt(3)h`
`=> x = sqrt(3)h - 60` ...(1)
Similarly in right ΔANB,
`tan 60^circ = (AB)/(NB)`
`tan 60^circ = h/(60 + x)`
`=> sqrt(3) = h/x`
`=> x = h/sqrt(3)` ...(2)
From (1) and (2), we have,
`sqrt(3)h - 60 = h/sqrt(3)`
`=> 3h - 60sqrt(3) = h`
`=> 3h - h = 60sqrt(3)`
`=> 2h = 60sqrt(3)`
`=> h= (60sqrt(3))/(2)`
`=> h = 30sqrt(3) = 30 xx 1.732`
`=>` h = 51.96 m
∴ Height of the building = 51.96 = 52 m (approx)
RELATED QUESTIONS
Prove the following identities:
tan2 A – sin2 A = tan2 A . sin2 A
From the top of a light house 100 m high, the angles of depression of two ships are observed as 48° and 36° respectively. Find the distance between the two ships (in the nearest metre) if:
- the ships are on the same side of the light house,
- the ships are on the opposite sides of the light house.
A person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 m away from the bank, he finds the angle of elevation to be 30°. Find:
- the height of the tree, correct to 2 decimal places,
- the width of the river.
The length of the shadow of a tower standing on level plane is found to be 2y metres longer when the sun’s altitude is 30° than when it was 45°. Prove that the height of the tower is `y(sqrt(3) + 1)` metres.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60° and the angle of depression of the bottom of the tower is 30°. Find:
- the height of the tower, if the height of the pole is 20 m;
- the height of the pole, if the height of the tower is 75 m.
A 10 m high pole is kept vertical by a steel wire. The wire is inclined at an angle of 40° with the horizontal ground. If the wire runs from the top of the pole to the point on the ground where Its other end is fixed, find the lenqth of the wire.
Due to a heavy storm, a part of a banyan tree broke without separating from the main. The top of the tree touched the ground 15 m from the base making an angle of 45° with the ground. Calculate the height of the tree before it was broken.
The top of a palm tree having been broken by the wind struck the ground at an angle of 60° at a distance of 9m from the foot of the tree. Find the original height of the palm tree.
An aeroplane when flying at a height of 4km from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the aeroplanes at that instant.
From the top of a tower 60 m high, the angles of depression of the top and bottom of pole are observed to be 45° and 60° respectively. Find the height of the pole.

