Advertisements
Advertisements
Question
A man on the deck of a ship is 10 m above water level. He observes that the angle of elevation of the top of a cliff is 42° and the angle of depression of the base is 20°. Calculate the distance of the cliff from the ship and the height of the cliff.
Solution
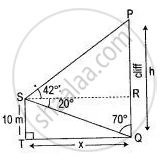
Let the height of the cliff be h meters and the distance of the cliff from the ship be x meters.
In right-angled ΔQRS,
∴ QR = ST = 10 m
TQ = RS = x m
∴ tan 70° = `"RS"/"QR"`
⇒ `2.747 = x/(10 m)`
∴ x = 27.47 m
Hence, the distance of the cliff from the ship = 27.47 m
Again in right angled ΔPRS,
∴ tan 42° = `"PR"/"RS"`
⇒ `0.9004 = "PR"/27.47`
⇒ PR = [ 0.9004 x 27.47 ] m
⇒ PR = 24.73 m
∴ PQ = PR + RQ
PQ = [ 24.73 + 10 ] m
PQ = 34.73 m
Hence the height of the cliff = 34.73 m.
APPEARS IN
RELATED QUESTIONS
A boy, 1.6 m tall, is 20 m away from a tower and observes the angle of elevation of the top of the tower to be (i) 45°, (ii) 60°. Find the height of the tower in each case.
Two vertical poles are on either side of a road. A 30 m long ladder is placed between the two poles. When the ladder rests against one pole, it makes angle 32°24′ with the pole and when it is turned to rest against another pole, it makes angle 32°24′ with the road. Calculate the width of the road.
Calculate BC.
An observer, 1.5m tall, is 28.5m away from a tower 30m high. Determine the angle of elevation of the top of the tower from his eye.
An observer point for ships moving in the sea 500m above the sea level. The person manning this point observes the angle of depression of twc boats as 45° and 30°. Find the distance between the boats when they are on the same side of the observation point and when they are on opposite sides of the observation point.
Of the two trees are on either side of a river, one of them is 50m high. From the top of this tree the angles of depression of the top and the foot of the other tree are 30° and 60° respectively. Find the width of the river and the height of the other tree.
A man standing on a cliff observes a ship at an angle of depression of the ship is 30°, approaching the shore just beneath him. Three minutes later, the angle of depression of the ship is 60°. How soon will it reach the shore?
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be α, and β. If the height of the light house is 'h' m and the line joining the ships passes through the foot of the light house, show that the distance between the ship is `("h"(tan α + tan β))/(tanα tanβ)`m.
A man on the top of vertical observation tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower? (Give your answer correct to nearest seconds).
A vertical tower standing on a horizontal plane is surmounted by a vertical flagstaff. At a point 100 m away from the foot of the tower, the angle of elevation of the top and bottom of the flagstaff are 54° and 42° respectively. Find the height of the flagstaff. Give your answer correct to nearest metre.

