Advertisements
Advertisements
Question
An observer point for ships moving in the sea 500m above the sea level. The person manning this point observes the angle of depression of twc boats as 45° and 30°. Find the distance between the boats when they are on the same side of the observation point and when they are on opposite sides of the observation point.
Solution
Case 1: When the boats are on same side of the observation point.
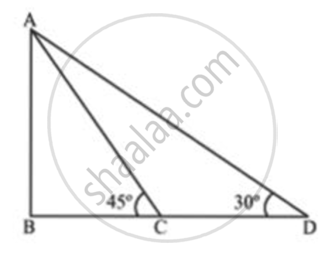
Let the position of the two ships be C and D. Let A be the point of observation.
AB = 500 m
In ΔBAC,
`tan45^circ = "AB"/"BC"`
⇒ `1 = 500/"BC"`
⇒ BC = 500 ....(1)
In ΔABD,
`tan30^circ = "AB"/"BD"`
⇒ `1/sqrt(3) = 500/"BD"`
⇒ `"BD" = 500sqrt(3)` ...(2)
From (1) and (2),
`"CD" = "BD" - "BC" = 500(sqrt(3) - 1) = 500 xx 0.732 = 366`
Thus, in this case, the distance between the boats is 366 m.
Case 2: When the boats are on different side of the observation point.
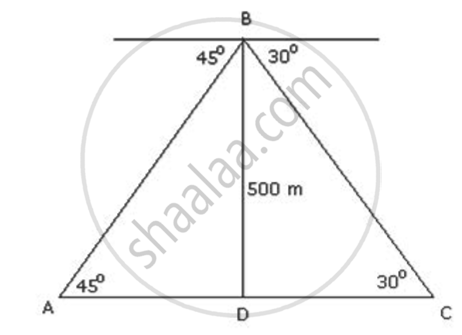
Let the position of the two ships be A and C. Let B be the point of observation.
In ΔBAD,
`tan45^circ = "BD"/"AD"`
⇒ `1 = 500/"AD"`
⇒ AD = 500 ....(1)
In ΔBDC,
`tan30^circ = "BD"/"DC"`
⇒ `1/sqrt(3) = 500/"DC"`
⇒ `"DC" = 500sqrt(3)` ....(2)
From (1) and (2),
`"AC" = "AD" + "DC" = 500 (1 + sqrt(3)) = 500 xx 2.732 = 1366`
Thus, in this case, the distance between the boats is 1366 m.
APPEARS IN
RELATED QUESTIONS
A bus covers a distance of 240 km at a uniform speed. Due to heavy rain, its speed gets reduced by 10 km/h and as such it takes two hrs longer to cover the total distance. Assuming the uniform speed to be ‘x’ km/h, form an equation and solve it to evaluate ‘x’.
A kite is attached to a string. Find the length of the string, when the height of the kite is 60 m and the string makes an angle 30° with the ground.
An aeroplane flying horizontally 1 km above the ground and going away from the observer is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°; find the uniform speed of the aeroplane in km per hour.
From a window A, 10 m above the ground the angle of elevation of the top C of a tower is x°, where tan `x^circ = 5/2` and the angle of depression of the foot D of the tower is y°, where tan `y^circ = 1/4`. Calculate the height CD of the tower in metres.
The topmost branch of a tree is tied with a string attached to a pole in the ground. The length of this string Is 200m and it makes an angle of 45° with the ground. Find the distance of the pole to which the string is tied from the base of the tree.
Find the angle of depression from the top of a 140m high pillar of a milestone on the ground at a distance of 200m from the foot of the pillar.
The height of an observation tower is 180m above sea level. A ship coming towards the tower is observed at an angle of depression of 30°. Calculate the distance of the boat from the foot of the observation tower.
From the top of a light house 96m high, the angles of depression of two ships in the river and at the same level as the base of the light house and on the same side of it, are α and β. If tan α = `1/4` and tan β = `1/7`, find the distance between the ships.
A man standing on a cliff observes a ship at an angle of depression of the ship is 30°, approaching the shore just beneath him. Three minutes later, the angle of depression of the ship is 60°. How soon will it reach the shore?
From a lighthouse, the angles of depression of two ships on opposite sides of the lighthouse were observed to be 30° and 45°. If the height of the lighthouse is 90 metres and the line joining the two ships passes through the foot of the lighthouse, find the distance between the two ships, correct to two decimal places.
